[TIL] 데이터분석 데브코스 48일차 (1) - 선형 SVM/소프트 마진 SVM/비선형 SVM/SVR(Support Vector Regression)

📌 학습목표

[분류 문제에 해결에 활용되는 알고리즘]
1. 선형 SVM
2. 비선형 SVM

[회귀 문제에 해결에 활용되는 알고리즘]
3. SVR(Support Vector Regression)

 

 

 

Q. "잘 나눈다"의 정의는 무엇일까?

• 정확히 나누었는가?
• 일반화가 잘 되었는가?

※ 일반화
: 유사한 데이터가 들어왔을 때 이들 사이의 전반적인 데이터 특성을 잘 고려한 상태

 

'일반화 성능이 좋다'의 의미

• 각 클래스를 잘 나누고 있을 뿐 아니라
• 각 클래스의 데이터 샘플로부터 가장 멀리 위치해 있는 상태

 

 

 

1. 선형 SVM

• 마진(margin) : 샘플로부터 분류 선까지의 거리
• 서포트 벡터(support vector) : 마진을 구성하는 데이터(마진 양쪽의 각각의 포인트)

 

 

선형 SVM의 목적

: 각 클래스를 분류하는 직선이 최대한 큰 마진을 갖고 있도록 하는 것

= 찾고자 하는 직선(혹은 초평면)과 평행한 두 개의 직선(혹은 초평면) 사이의 거리를 최대화화는 '최적 직선(최대 마진 초평면)'을 만드는 것

 

 

최대 마진 초평면의 선형 방정식

 

• `w` : 최대 마진 초평면의 법선 벡터(직선을 이루는 coefficient들의 합)
• `b` : 평향값(절편)

► 우리의 목표는 학습을 통해 w와 b를 찾는 것!

 

 

 

선형 SVM 수식적 표현

• 평행한 두 직선 위에 존재하는 서포트 벡터들에 대해서 다음을 만족한다 : 
  
• 서포트 벡터보다 위/아래 쪽 영역에 대해서 다음을 만족한다 : 
  
• 평행한 두 직선 사이 공간인 '마진'에 대해서 다음을 만족한다 : 
  

 

 

선형 SVM 최적화 문제

최적화 목표 : 마진을 최대화하면서 모든 데이터를 정확히 분류하는 것

 

 

 

► 라그랑주 승수법과 쌍대 문제 방식으로 문제를 해결해야 함

 

 

 

선형 SVM의 유형

1. 하드 마진 SVM

: 어떤 오분류도 허용하지 않는 완벽한 선형 모델로 분리

 

2. 소프트 마진 SVM

: 어느 정도의 오분류는 허용하면서 오차 발생에 따른 패널티를 비용함수에 부과 ► 일반화 성능 향상 가능

(최적화 문제 관점에서는 패널티를 줄이는 방향으로 문제 해결)

 

 

 

 

 

소프트 마진 SVM

목표 : 슬랙 변수가 최소화되는 방향으로 만드는 것

 

슬랙 변수(slack variable)

: 마진(넘지 말아야 할 경계)을 얼마나 위반하는지(넘었는지)를 수치적으로 나타낸 변수

• 모든 각 데이터 포인트(i) 하나하나에 부여됨
• 완벽하게 선형 분리되지 않는 데이터에 대해 SVM을 적용할 수 있도록 함

 

• 마진을 위반하지 않은 데이터 : 𝜉i =0
  • 서포트 벡터
  • 서포트 벡터보다 멀리 있는 데이터
• 마진을 위반한 데이터
  • 마진경계 ~ 결정경계 : 0 < 𝜉i ≤ 1
  • 결정경계 이후 : 1 < 𝜉i ← 이 경우는 올바르지 못한 클래스로 분류됨

 

 

소프트 마진 SVM의 최적화 함수

하드 마진 SVM 최적화 과정에 규제 페널티(𝜉#)를 도입해 일반화한 최적화 식을 사용

 

목적 :

1. 마진의 크기를 최대화
2. 마진 위반(=패널티)를 최소화

 

• 𝐶 : 일반화를 위한 하이퍼 파라미터로, 마진 크기와 규제 사이의 중요도 변수(패널티를 얼마나 강하게 부여할 것이냐에 대한 상수)
• 1 − 𝜉i : 규제가 적용될 데이터 포인트에 대해, 결정경계에서 𝜉i의 거리만큼 벗어날 수 있음을 허용하는 과정
• 𝜉i ≥ 0 : "𝜉i가 음수를 가질 수 없음" 을 조건으로 제시

 

 

하드 마진 SVM 실습

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.svm import SVC

seed = 1234
np.random.seed(seed)

 

# 데이터 생성
X1, y1 = make_classification(n_samples=100, # 생성할 데이터 수
                             n_features=2, # 사용할 특성의 수
                             n_redundant=0, # 중복 특성(다른 특성으로부터 파생된 특성) 수 : 상관관계를 얼마나 줄 것인가
                             n_clusters_per_class=1, # 클래스 당 클러스터의 수 : 군집이 몇 개인가
                             flip_y=0, #  클래스 레이블이 뒤바뀔 확률, 노이즈에 해당 (0이면 하드 마진 SVM)
                             class_sep=2, # 클래스 간 분리도를 조절, 높을수록 분리가 잘 됨을 의미
                             random_state=5)

 

# 데이터 시각화
plt.scatter(X1[:, 0], X1[:, 1], c=y1, cmap=plt.cm.Paired)

plt.xlabel('feature1')
plt.ylabel('featuer2')

plt.margins(0.2)

plt.show()

svm_hard_margin = SVC(kernel='linear', C=1000) # C : 슬랙변수
svm_hard_margin.fit(X1, y1)

 

plt.scatter(X1[:, 0], X1[:, 1], c=y1, cmap=plt.cm.Paired)

plt.xlabel('feature1')
plt.ylabel('featuer2')

plt.margins(0.2)

# 현재 그래프의 x축과 y축 범위를 가져옴
xlim = plt.gca().get_xlim()
ylim = plt.gca().get_ylim()

# 그래프의 x & y축 범위를 바탕으로 모든 x,y 조합의 좌표 그리드를 생성
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 50),
                     np.linspace(ylim[0], ylim[1], 50))

# 그리드 포인트를 이용해 각 포인트에서의 Desicion 결과값을 출력
Z = svm_hard_margin.decision_function(
    np.column_stack(
        (xx.ravel(), # xx matrix를 1차원 행렬로 flatten
        yy.ravel())  # yy matrix를 1차원 행렬로 flatten
     ) # 1 차원 행렬을 열 방향으로 묶어줌
) # 입력된 각 (x, y) 포인트에 대해 결정 경계로부터의 거리를 계산
Z = Z.reshape(xx.shape)

# 결정 경계와 마진 직선을 그리는 함수
plt.contour(xx, yy, # xx와 yy 공간 안에
            Z, # Z를 그릴건데
            levels=[-1, 0, 1], # Z가 -1, 0, 1 인 부분만 그릴것!
            colors=['orange', 'blue', 'orange'],
            alpha=0.5, # 투명도
            linestyles=['--', '-', '--'] # -1, 0, 1 의 직선 개형을 표시
)

 

 

 

 

소프트 마진 SVM 실습

# 데이터 생성
X2, y2 = make_classification(n_samples=100, # 생성할 데이터 수
                             n_features=2, # 사용할 특성의 수
                             n_redundant=0, # 중복 특성(다른 특성으로부터 파생된 특성) 수
                             n_clusters_per_class=1, # 클래스 당 클러스터의 수
                             flip_y=0.06, #  클래스 레이블이 뒤바뀔 확률, 노이즈에 해당
                             class_sep=1.5, # 클래스 간 분리도를 조절, 높을수록 분리가 잘 됨을 의미
                             random_state=5)

 

# 데이터 시각화
plt.scatter(X2[:, 0], X2[:, 1], c=y2, cmap=plt.cm.Paired)

plt.xlabel('feature1')
plt.ylabel('featuer2')

plt.margins(0.2)

plt.show()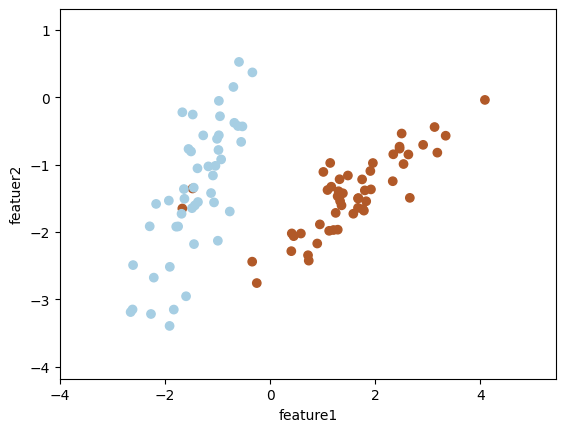

svm_soft_margin = SVC(kernel='linear', C=0.1)
svm_soft_margin.fit(X2, y2)

 

plt.scatter(X2[:, 0], X2[:, 1], c=y2, cmap=plt.cm.Paired)

plt.xlabel('feature1')
plt.ylabel('featuer2')

plt.margins(0.2)

# 현재 그래프의 x축과 y축 범위를 가져옴
xlim = plt.gca().get_xlim()
ylim = plt.gca().get_ylim()

# 그래프의 x & y축 범위를 바탕으로 모든 x,y 조합의 좌표 그리드를 생성
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 50),
                     np.linspace(ylim[0], ylim[1], 50))

# 그리드 포인트를 이용해 각 포인트에서의 Desicion 결과값을 출력
Z = svm_soft_margin.decision_function(
    np.column_stack(
        (xx.ravel(), # xx matrix를 1차원 행렬로 flatten
        yy.ravel())  # yy matrix를 1차원 행렬로 flatten
     ) # 1 차원 행렬을 열 방향으로 묶어줌
) # 입력된 각 (x, y) 포인트에 대해 결정 경계로부터의 거리를 계산
Z = Z.reshape(xx.shape)

# 결정 경계와 마진 직선을 그리는 함수
plt.contour(xx, yy, # xx와 yy 공간 안에
            Z, # Z를 그릴건데
            levels=[-1, 0, 1], # Z가 -1, 0, 1 인 부분만 그릴것!
            colors=['orange', 'blue', 'orange'],
            alpha=0.5,
            linestyles=['--', '-', '--'] # -1, 0, 1 의 직선 개형을 표시
)

def plot_svm_decision_boundary(svm_model, X, y, title):
    """Plot the decision boundary of an SVM model."""
    svm_model.fit(X, y)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)

    plt.xlabel('feature1')
    plt.ylabel('feature2')
    plt.margins(0.2)

    xlim = plt.gca().get_xlim()
    ylim = plt.gca().get_ylim()

    xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 50), np.linspace(ylim[0], ylim[1], 50))

    Z = svm_model.decision_function(np.column_stack((xx.ravel(), yy.ravel())))
    Z = Z.reshape(xx.shape)

    plt.contour(xx, yy, Z, levels=[-1, 0, 1], colors=['orange', 'blue', 'orange'], alpha=0.5, linestyles=['--', '-', '--'])
    plt.title(title)

# 서로 다른 규제 변수를 갖는 3개의 모델 생성
svm_C_0_1 = SVC(kernel='linear', C=0.1)
svm_C_1 = SVC(kernel='linear', C=1)
svm_C_1000 = SVC(kernel='linear', C=1000)

# 시각화
plt.figure(figsize=(18, 6))

plt.subplot(1, 3, 1)
plot_svm_decision_boundary(svm_C_0_1, X2, y2, "SVM with C=0.1")

plt.subplot(1, 3, 2)
plot_svm_decision_boundary(svm_C_1, X2, y2, "SVM with C=1")

plt.subplot(1, 3, 3)
plot_svm_decision_boundary(svm_C_1000, X2, y2, "SVM with C=1000")

plt.show()

 

 

► `C`(슬랙변수 값)가 커짐에 따라 결정 경계가 좁아지는 것을 알 수 있다. ► 일반화 성능이 떨어질 수 있음

 

 

 

 

선형 SVM 모델의 한계

데이터가 훨씬 더 복잡해지면 선형 결정 경계(일직선)으로 데이터를 분류할 수 없는 경우가 발생

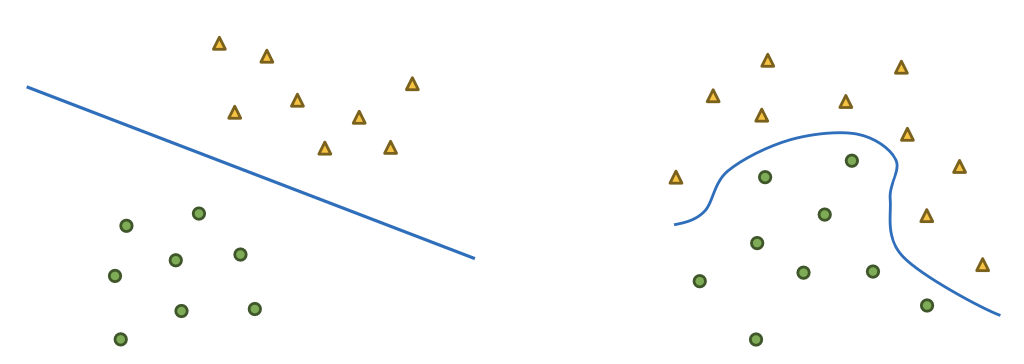
► 해결 방법 : 비선형 SVM

 

 

 

 

---

2. 비선형 SVM

저차원보다 고차원 데이터일수록 선형으로 분류할 수 있는 가능성이 높아짐

• 차원이 증가하면 데이터 포인트 간의 상대거리는 증가
• 각 차원에서 데이터끼리 차지하는 공간이 확장
• 그러면서 비슷한 특성을 공유하는 데이터들은 특정한 축 혹은 방향으로 군집될 가능성이 ↑
• 데이터를 선형 분류하기 위해서는 데이터 포인트 사이의 내적 계산이 수행되어야 함
   

 

매핑 함수(Mapping function; 𝜙)

: 저차원의 데이터를 고차원의 데이터로 옮기는 함수

 

 

 

커널(kernel)

: 데이터를 고차원으로 보내서 내적 계산하면 계산량이 부담스러우므로, 저차원에 있는 데이터만으로 고차원 데이터를 활용한 내적 연산과 똑같은 결과를 보여주는 함수

 

커널의 종류

1. 다항 커널 (Polynomial Kernel)

: 일차식을 마치 다항식으로 보냈을때의 효과를 보여줌

• 다양한 차수 설정으로 여러 식 근사 가능
• 과적합 위험 존재

 

 

 

2. RBF 커널 (Radial Basis Funciton Kernel) (혹은 가우시안 커널 Gaussian Kernel)

: 두 데이터 포인트 간의 거리를 가우시안 함수에 넣음

• 다양한 데이터에 적용 가능
• 유연성이 좋아서 범용성이 높음

 

 

 

3. 시그모이드 커널 (Sigmoid Kernel)

: 이진 분류에 최적화되며 RBF 커널에 비해 성능이 떨어짐

 

 

 

 

 

 

비선형 SVM의 최적화 문제

: 소프트 마진 SVM 최적화 식에 고차원에서의 데이터 분류가 가능하도록 조건만 변경한 형태

► 라그랑주 승수법과 쌍대 문제 방식으로 문제를 해결해야 함

 

 

 

비선형 SVM 실습

from sklearn.datasets import make_moons

# 데이터 생성
X_moons, y_moons = make_moons(n_samples=100, noise=0.15, random_state=0)

# 시각화
plt.figure(figsize=(6, 5))
plt.scatter(X_moons[:, 0], X_moons[:, 1], c=y_moons, cmap=plt.cm.Paired)
plt.title("Moon Shaped Data")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()

# 비선형 SVM 으로 분류

# 선형 커널
Linear_SVM = SVC(kernel='linear')
# 다항 커널
Poly_SVM = SVC(kernel='poly', degree=3)
# RBF 커널
RBF_SVM = SVC(kernel='rbf')
# Sigmoid 커널
sigmoid_SVM = SVC(kernel='sigmoid')

# 시각화
plt.figure(figsize=(10, 10))

plt.subplot(2, 2, 1)
plot_svm_decision_boundary(Linear_SVM, X_moons, y_moons, "Linear SVM")

plt.subplot(2, 2, 2)
plot_svm_decision_boundary(Poly_SVM, X_moons, y_moons, "Polynomial SVM")

plt.subplot(2, 2, 3)
plot_svm_decision_boundary(RBF_SVM, X_moons, y_moons, "RBF SVM")

plt.subplot(2, 2, 4)
plot_svm_decision_boundary(sigmoid_SVM, X_moons, y_moons, "Sigmoid SVM")

 

 

 

 

 

 

 

 

 

 

 

---

3. SVR (Support Vector Regression)

: 회귀 문제로 확장한 SVM 방법

 

목표

: 주어진 데이터들을 가지고 데이터를 잘 표현하는 회귀 직선을 만드는 것

 

• 주어진 데이터에서 가능한 많은 데이터 포인트를 포함하는 마진 구역을 설정
• 마진 구역은 사용자가 선언한 허용오차(𝜀) 내부의 구역
• 그 마진 구역 안에서 회귀선(혹은초평면)을 찾는것

 

 

 

 

SVR의 최적화 문제

목표 : 오차를 포함해서 슬랙변수가 최소화되는 방향으로 데이터를 최대한 많이 포함하는 것

 

► 라그랑주 승수법과 쌍대 문제 방식으로 문제를 해결해야 함

 

 

 

 

SVR 실습

# 데이터 생성 변수
w0 = 2.3
w1 = 3.5
num_data = 100
noise = np.random.normal(0, 6, num_data)

# 데이터 생성
x = np.linspace(0, 10, num_data)
y = w0 + w1 * x + noise

# 시각화
plt.scatter(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.margins(0.2)
plt.show()

 

from sklearn.svm import SVR

epsilon = 5 # 허용 오차

# SVR 객체 생성
svr_linear = SVR(kernel='linear', epsilon=epsilon)
svr_poly = SVR(kernel='poly', degree=3, epsilon=epsilon) # 3차 다항식으로
svr_rbf = SVR(kernel='rbf', epsilon=epsilon)
svr_sigmoid = SVR(kernel='sigmoid', epsilon=epsilon)

# SVR 모델 학습
svr_linear.fit(x.reshape(-1, 1), y)
svr_poly.fit(x.reshape(-1, 1), y)
svr_rbf.fit(x.reshape(-1, 1), y)
svr_sigmoid.fit(x.reshape(-1, 1), y)

# 그림을 그리기 위한 X 좌표 생성
x_range = np.linspace(x.min(), x.max(), 100).reshape(-1, 1)

# X 좌표에 대한 Y 출력 결과 도출
y_linear = svr_linear.predict(x_range)
y_poly = svr_poly.predict(x_range)
y_rbf = svr_rbf.predict(x_range)
y_sigmoid = svr_sigmoid.predict(x_range)

plt.figure(figsize=(12, 12))

# Linear 커널
plt.subplot(2, 2, 1)
plt.scatter(x, y)
plt.plot(x_range, y_linear, color='red')
plt.fill_between(x_range.ravel(), y_linear - svr_linear.epsilon, y_linear + svr_linear.epsilon, color='red', alpha=0.2)
plt.title("Linear SVR")
plt.xlabel('x')
plt.ylabel('y')

# Polynomial 커널
plt.subplot(2, 2, 2)
plt.scatter(x, y)
plt.plot(x_range, y_poly, color='red')
plt.fill_between(x_range.ravel(), y_poly - svr_poly.epsilon, y_poly + svr_poly.epsilon, color='red', alpha=0.2)
plt.title("Polynomial SVR")
plt.xlabel('x')
plt.ylabel('y')

# RBF 커널
plt.subplot(2, 2, 3)
plt.scatter(x, y)
plt.plot(x_range, y_rbf, color='red')
plt.fill_between(x_range.ravel(), y_rbf - svr_rbf.epsilon, y_rbf + svr_rbf.epsilon, color='red', alpha=0.2)
plt.title("RBF SVR")
plt.xlabel('x')
plt.ylabel('y')

# Sigmoid 커널
plt.subplot(2, 2, 4)
plt.scatter(x, y)
plt.plot(x_range, y_sigmoid, color='red')
plt.fill_between(x_range.ravel(), y_sigmoid - svr_sigmoid.epsilon, y_sigmoid + svr_sigmoid.epsilon, color='red', alpha=0.2)
plt.title("Sigmoid SVR")
plt.xlabel('x')
plt.ylabel('y')

plt.tight_layout()
plt.show()