🔗 실습 링크 : https://www.kaggle.com/datasets/sjleshrac/airlines-customer-satisfaction
Airlines Customer satisfaction
Customer satisfaction with various other factors
www.kaggle.com
SVM을 활용한 풀이
1단계. 데이터 로드 및 전처리
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
seed = 1234
np.random.seed(seed)
# 데이터 로드
data_path = '/content/Invistico_Airline.csv'
airplane = pd.read_csv(data_path)- NA값제거
- 지연시간5시간이상제거
- 범주형 데이터 인코딩
- 상관도를 바탕으로 15개 특성 추출
- 20%기준으로 학습 및 평가데이터 분할
# 데이터 자료형에 따른 column 구분
y_column = ['satisfaction']
numeric_columns = ['Age', 'Flight Distance',
'Departure Delay in Minutes', 'Arrival Delay in Minutes']
ordinal_columns = ['Seat comfort', 'Departure/Arrival time convenient',
'Food and drink', 'Gate location',
'Inflight wifi service', 'Inflight entertainment',
'Online support', 'Ease of Online booking',
'On-board service', 'Leg room service',
'Baggage handling', 'Checkin service',
'Cleanliness', 'Online boarding']
category_columns = ['Gender', 'Customer Type',
'Type of Travel', 'Class']
# na값 제거
airplane_cleaned = airplane.dropna()
# 지연 시간 5시간 이상은 제거
time_limit = 300
airplane_cleaned = airplane_cleaned[(airplane_cleaned['Arrival Delay in Minutes'] < time_limit) &
(airplane_cleaned['Departure Delay in Minutes'] < time_limit)]
# 카테고리형 변수 인코딩
airplane_cate_encoded = pd.get_dummies(airplane_cleaned[category_columns], drop_first=True)
airplane_target_encoded = pd.get_dummies(airplane_cleaned[y_column], drop_first=True)
airplane_combined = pd.concat([airplane_target_encoded,
airplane_cleaned[numeric_columns + ordinal_columns],
airplane_cate_encoded],
axis=1)
# 상관 관계를 바탕으로 15개의 특징만 추출
# 추출할 특징의 이름 ↓
y_column = ['satisfaction_satisfied']
ext_ordinal_columns = ['Inflight entertainment', 'Ease of Online booking',
'Online support', 'On-board service',
'Online boarding', 'Leg room service',
'Checkin service', 'Baggage handling',
'Cleanliness', 'Seat comfort',
'Inflight wifi service', 'Food and drink']
ext_category_columns = ['Customer Type_disloyal Customer', 'Class_Eco',
'Gender_Male']
# 추출된 특징만을 포함할 데이터
ext_airplane_combined = airplane_combined[y_column + ext_ordinal_columns + ext_category_columns]
# 학습 및 평가 데이터 분리
X = ext_airplane_combined.drop(y_column, axis=1)
y = ext_airplane_combined[y_column]
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.2,
random_state=42)X_train.info()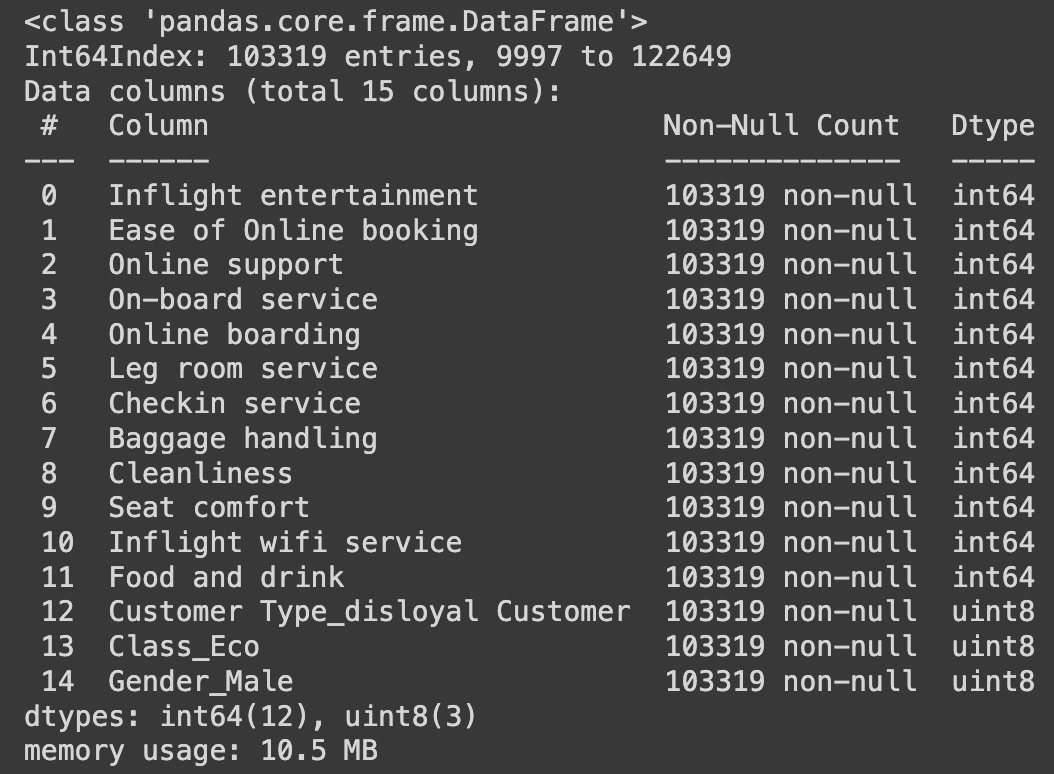
📌 하나의 셀을 실행시킬 때 얼만큼 시간이 걸렸는지 측정해주는 매직 키워드
%%timeit
► `854 ms ± 21.5 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)`
- 1개의 루프 안에 7번의 fitting 실행이 있었음
- 약 854 ms 정도의 시간이 걸림
2단계. SVM 모델을 활용한 학습
- RBF 커널 사용
- 슬랙 변수 `C = 0.1`로 설정
- SVM은 원래 시간이 매우 오래 걸린다. (실습 데이터 기준 약 30분 소요)
- SVM의 시간복잡도 :
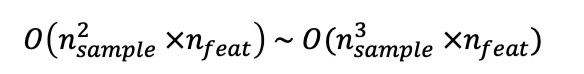
from sklearn.svm import SVC
svm = SVC(kernel='rbf', C=0.1)
%%timeit
svm.fit(X_train, y_train)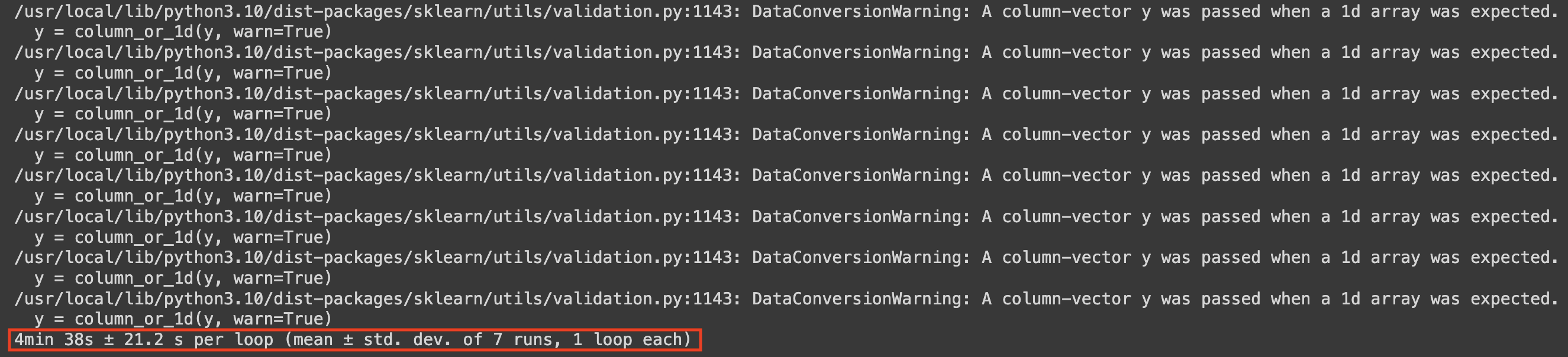
3단계. 학습 SVM 모델을 활용한 예측 및 평가 진행
# 예측 수행
y_train_pred_svm = svm.predict(X_train)
y_test_pred_svm = svm.predict(X_test)
# 평가 지표 계산: 정확도 (맞은수/전체)
acc_train = accuracy_score(y_train, y_train_pred_svm)
acc_test = accuracy_score(y_test, y_test_pred_svm)
print(f'학습 데이터를 이용한 SVM Acc 값 : {acc_train*100:.1f}%')
print(f'평가 데이터를 이용한 SVM Acc 값 : {acc_test*100:.1f}%')
► 로지스틱 회귀 모델을 사용했을 때 평가 데이터를 활용한 정확도가 82.9% 였던것에 비하면 성능이 매우 향상된 것을 알 수 있다.
# confusion matrix을 활용한 평가 결과 확인
cm_test_svm = confusion_matrix(y_test, y_test_pred_svm)
plt.imshow(cm_test_svm, interpolation='nearest', cmap='Blues')
plt.title("SVM Confusion Matrix (Test)")
plt.colorbar()
tick_marks = np.arange(len(np.unique(y_test)))
plt.xticks(tick_marks, np.unique(y_test))
plt.yticks(tick_marks, np.unique(y_test))
plt.xlabel("Predicted Label")
plt.ylabel("True Label")
# 각 셀에 숫자 표시
for i in range(cm_test_svm.shape[0]):
for j in range(cm_test_svm.shape[1]):
plt.text(j, i, cm_test_svm[i, j], ha="center", va="center", color="black")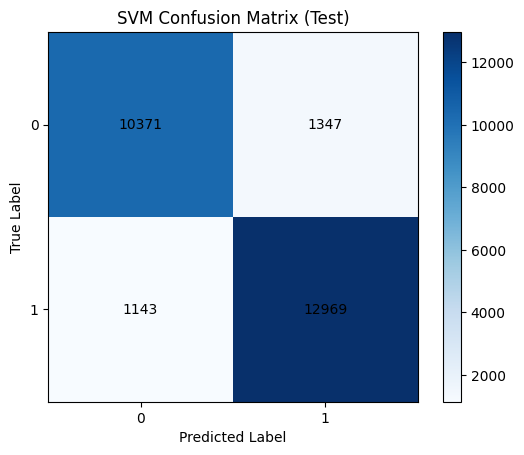
# 정밀도, 재현율, F1 값 비교
from sklearn.metrics import precision_score, recall_score, f1_score
logistic_precision = precision_score(y_test, y_test_pred_logis)
logistic_recall = recall_score(y_test, y_test_pred_logis)
logistic_f1 = f1_score(y_test, y_test_pred_logis)
print(f'Logistic의 P,R,F1 : {logistic_precision:.2f} / {logistic_recall:.2f} / {logistic_f1:.2f}')
svm_precision = precision_score(y_test, y_test_pred_svm)
svm_recall = recall_score(y_test, y_test_pred_svm)
svm_f1 = f1_score(y_test, y_test_pred_svm)
print(f'SVM의 P,R,F1 : {svm_precision:.2f} / {svm_recall:.2f} / {svm_f1:.2f}')
► 로지스틱 회귀보다 SVM 모델을 활용한 예측이 훨씬 더 정확하다고 해석할 수 있다.
※ 분류 평가 척도 - 정밀도 / 재현율 / F1 점수
1. 정밀도 (Precision)
- 예측한 양성 결과가 실제로 얼마나 진짜 양성인지를 계산
- 모델이 양성 결과를 잘 찾아내야 하는 상황에서 중요
2. 재현율 (Recall)
- 실제 양성 중 얼마나 양성을 잘 찾아냈는지를 계산
- 정답을 잘 찾아내는 과정에서 중요
※ 정밀도와 재현율은 서로 Trade-off 관계
'(엄청 신중하게)이것은 정답일 수 밖에 없다.' 라고 판단한 것들만 양성이라고 얘기하면 정밀도는 늘어난다.
반면, 재현율은 떨어진다. (∵ 딱 봐도 정답인데 정답이라고 안하고 신중하게 판단 후에 정답이라고 하니까)
3. F1 Score
- 정밀도와 재현율의 조화 평균
- 조화평균을 사용해 낮음 점수에 대한 패널티를 늘림
- 정밀도와 재현율이 전반적으로 좋아야 좋은 F1값을 갖을 수 있음
Decision Tree를 활용한 풀이
- 엔트로피 결정 경계 사용
- 트리의 최대 깊이 `max_depth = 5`로 설정
- SVM에 비해 학습 속도가 빠름 (트리 깊이에 따라 변동성이 크긴함)
- DT의 시간 복잡도 :
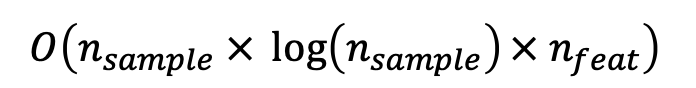
1단계. Decision Tree 모델을 활용한 학습
from sklearn.tree import DecisionTreeClassifier
dt = DecisionTreeClassifier(criterion='entropy',
max_depth=5,
min_samples_split=5)
%%timeit
dt.fit(X_train, y_train)
from sklearn.tree import plot_tree
plt.figure(figsize=(100, 20))
plot_tree(dt, filled=True,
feature_names=ext_ordinal_columns + ext_category_columns,
class_names=['satisfied', 'unsatisfied'])
plt.title("Plot of Decision Tree")
plt.show()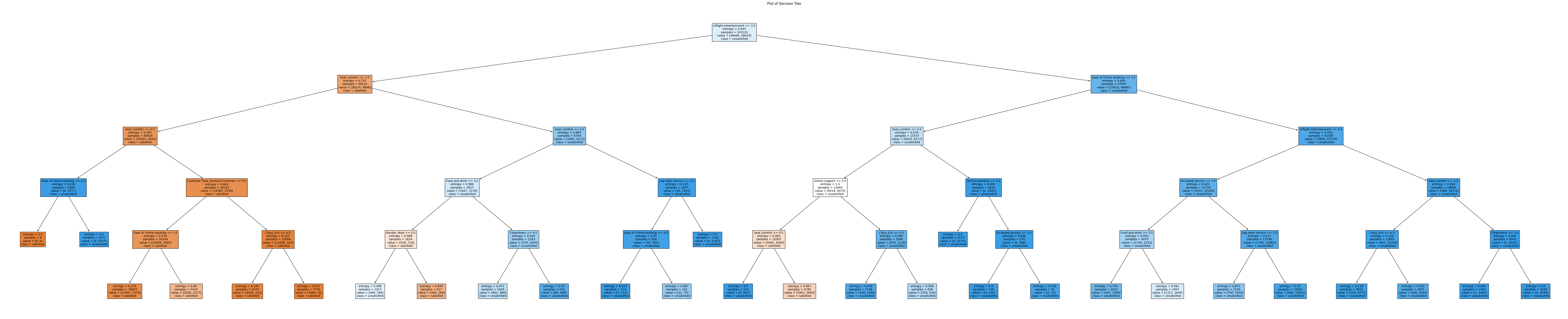
머신 러닝 모델의 크기가 커지고 복잡도가 증가하면 모델의 성능은 올라간다.
하지만, 과적합이 발생하며 오히려 성능이 하락하기도 한다.
∴ 평가 데이터에 대한 성능이 낮아지기 시작하는 지점의 세팅을 이용해 최적의 모델을 선택하는 것이 바람직하다
2단계. max_depth를 조절하면서 최적의 모델 찾기
# max depth에 따른 학습 결과 경향성 파악
max_depths = range(3, 30)
# 훈련 데이터 정확도와 테스트 데이터 정확도를 각각 빈 리스트로 만들고
# for문을 3부터 30까지 돌면서 최고의 모델을 찾는 방식으로 알고리즘 작성
train_accuracies = []
test_accuracies = []
for depth in max_depths:
model = DecisionTreeClassifier(criterion='entropy',
max_depth=depth,
min_samples_split=5)
model.fit(X_train, y_train)
# 학습 데이터에 대한 정확도
y_train_pred = model.predict(X_train)
train_acc = accuracy_score(y_train, y_train_pred)
train_accuracies.append(train_acc)
# 평가 데이터에 대한 정확도
y_test_pred = model.predict(X_test)
test_acc = accuracy_score(y_test, y_test_pred)
test_accuracies.append(test_acc)
# 결과 시각화
plt.figure(figsize=(10, 6))
plt.plot(max_depths, train_accuracies, label='Training Accuracy')
plt.plot(max_depths, test_accuracies, label='Test Accuracy')
plt.xlabel('Max Depth')
plt.ylabel('Accuracy')
plt.title('Decision Tree Accuracy vs Max Depth')
plt.legend()
plt.show()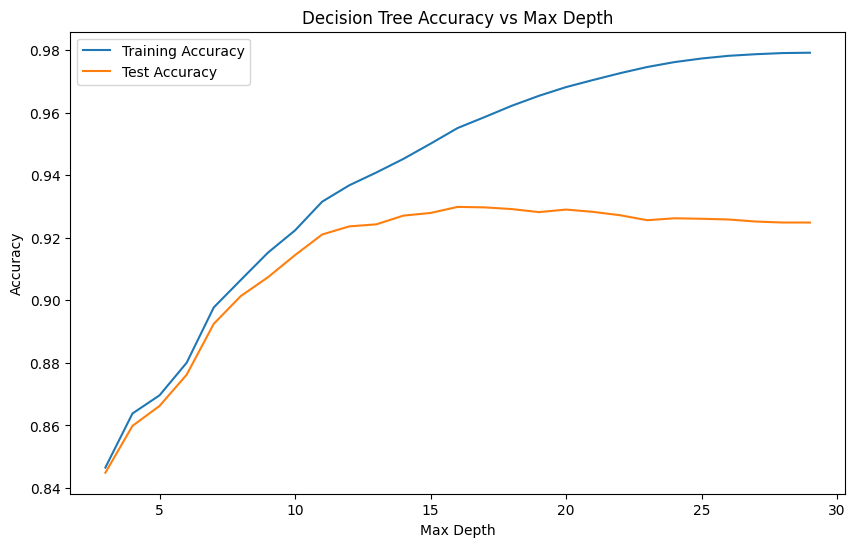
# 최대 정확도를 달성하는 max_depth를 찾고 해당 depth로 최적 모델 학습
max_acc = max(test_accuracies)
best_depth = max_depths[test_accuracies.index(max_acc)]
print('최대 정확도의 depth :', best_depth)
dt = DecisionTreeClassifier(criterion='entropy',
max_depth=best_depth,
min_samples_split=5)
# 예측 수행
y_train_pred_dt = dt.predict(X_train)
y_test_pred_dt = dt.predict(X_test)
# 평가 지표 계산: 정확도 (맞은수/전체)
acc_train = accuracy_score(y_train, y_train_pred_dt)
acc_test = accuracy_score(y_test, y_test_pred_dt)
print(f'학습 데이터를 이용한 DT Acc 값 : {acc_train*100:.1f}%')
print(f'평가 데이터를 이용한 DT Acc 값 : {acc_test*100:.1f}%')
► 최적의 `max_depth = 16` 인 것을 찾고 이를 모델에 적용 시킨 결과, 정확도가 확연히 높아진 것을 알 수 있다.
# confusion matrix을 활용한 평가 결과 확인
cm_test_dt = confusion_matrix(y_test, y_test_pred_dt)
plt.imshow(cm_test_dt, interpolation='nearest', cmap='Blues')
plt.title("Decision Tree Confusion Matrix (Test)")
plt.colorbar()
tick_marks = np.arange(len(np.unique(y_test)))
plt.xticks(tick_marks, np.unique(y_test))
plt.yticks(tick_marks, np.unique(y_test))
plt.xlabel("Predicted Label")
plt.ylabel("True Label")
# 각 셀에 숫자 표시
for i in range(cm_test_dt.shape[0]):
for j in range(cm_test_dt.shape[1]):
plt.text(j, i, cm_test_dt[i, j], ha="center", va="center", color="black")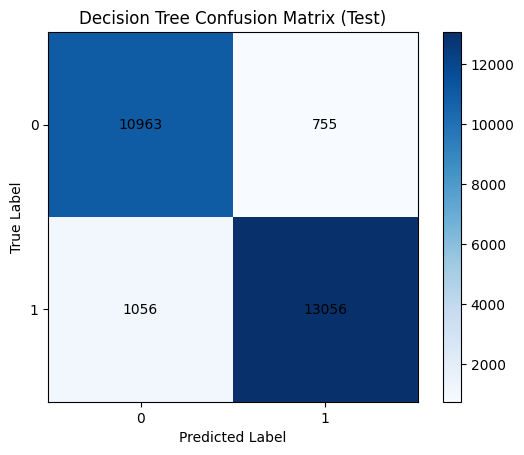
3단계. 각각 로지스틱, SVM, DT를 활용했을 때의 성능 비교해보기
# 정밀도, 재현율, F1 값 비교
from sklearn.metrics import precision_score, recall_score, f1_score
logistic_precision = precision_score(y_test, y_test_pred_logis)
logistic_recall = recall_score(y_test, y_test_pred_logis)
logistic_f1 = f1_score(y_test, y_test_pred_logis)
print(f'Logistic의 P,R,F1 : {logistic_precision:.2f} / {logistic_recall:.2f} / {logistic_f1:.2f}')
svm_precision = precision_score(y_test, y_test_pred_svm)
svm_recall = recall_score(y_test, y_test_pred_svm)
svm_f1 = f1_score(y_test, y_test_pred_svm)
print(f'SVM의 P,R,F1 : {svm_precision:.2f} / {svm_recall:.2f} / {svm_f1:.2f}')
dt_precision = precision_score(y_test, y_test_pred_dt)
dt_recall = recall_score(y_test, y_test_pred_dt)
dt_f1 = f1_score(y_test, y_test_pred_dt)
print(f'DT의 P,R,F1 : {dt_precision:.2f} / {dt_recall:.2f} / {dt_f1:.2f}')
'데이터 분석 Data Analytics > 프로그래머스 데이터분석 데브코스 2기' 카테고리의 다른 글
🔗 실습 링크 : https://www.kaggle.com/datasets/sjleshrac/airlines-customer-satisfaction
Airlines Customer satisfaction
Customer satisfaction with various other factors
www.kaggle.com
SVM을 활용한 풀이
1단계. 데이터 로드 및 전처리
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
seed = 1234
np.random.seed(seed)
# 데이터 로드
data_path = '/content/Invistico_Airline.csv'
airplane = pd.read_csv(data_path)- NA값제거
- 지연시간5시간이상제거
- 범주형 데이터 인코딩
- 상관도를 바탕으로 15개 특성 추출
- 20%기준으로 학습 및 평가데이터 분할
# 데이터 자료형에 따른 column 구분
y_column = ['satisfaction']
numeric_columns = ['Age', 'Flight Distance',
'Departure Delay in Minutes', 'Arrival Delay in Minutes']
ordinal_columns = ['Seat comfort', 'Departure/Arrival time convenient',
'Food and drink', 'Gate location',
'Inflight wifi service', 'Inflight entertainment',
'Online support', 'Ease of Online booking',
'On-board service', 'Leg room service',
'Baggage handling', 'Checkin service',
'Cleanliness', 'Online boarding']
category_columns = ['Gender', 'Customer Type',
'Type of Travel', 'Class']
# na값 제거
airplane_cleaned = airplane.dropna()
# 지연 시간 5시간 이상은 제거
time_limit = 300
airplane_cleaned = airplane_cleaned[(airplane_cleaned['Arrival Delay in Minutes'] < time_limit) &
(airplane_cleaned['Departure Delay in Minutes'] < time_limit)]
# 카테고리형 변수 인코딩
airplane_cate_encoded = pd.get_dummies(airplane_cleaned[category_columns], drop_first=True)
airplane_target_encoded = pd.get_dummies(airplane_cleaned[y_column], drop_first=True)
airplane_combined = pd.concat([airplane_target_encoded,
airplane_cleaned[numeric_columns + ordinal_columns],
airplane_cate_encoded],
axis=1)
# 상관 관계를 바탕으로 15개의 특징만 추출
# 추출할 특징의 이름 ↓
y_column = ['satisfaction_satisfied']
ext_ordinal_columns = ['Inflight entertainment', 'Ease of Online booking',
'Online support', 'On-board service',
'Online boarding', 'Leg room service',
'Checkin service', 'Baggage handling',
'Cleanliness', 'Seat comfort',
'Inflight wifi service', 'Food and drink']
ext_category_columns = ['Customer Type_disloyal Customer', 'Class_Eco',
'Gender_Male']
# 추출된 특징만을 포함할 데이터
ext_airplane_combined = airplane_combined[y_column + ext_ordinal_columns + ext_category_columns]
# 학습 및 평가 데이터 분리
X = ext_airplane_combined.drop(y_column, axis=1)
y = ext_airplane_combined[y_column]
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.2,
random_state=42)X_train.info()
📌 하나의 셀을 실행시킬 때 얼만큼 시간이 걸렸는지 측정해주는 매직 키워드
%%timeit
► 854 ms ± 21.5 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
- 1개의 루프 안에 7번의 fitting 실행이 있었음
- 약 854 ms 정도의 시간이 걸림
2단계. SVM 모델을 활용한 학습
- RBF 커널 사용
- 슬랙 변수
C = 0.1로 설정 - SVM은 원래 시간이 매우 오래 걸린다. (실습 데이터 기준 약 30분 소요)
- SVM의 시간복잡도 :
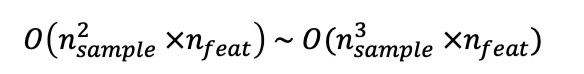
from sklearn.svm import SVC
svm = SVC(kernel='rbf', C=0.1)
%%timeit
svm.fit(X_train, y_train)
3단계. 학습 SVM 모델을 활용한 예측 및 평가 진행
# 예측 수행
y_train_pred_svm = svm.predict(X_train)
y_test_pred_svm = svm.predict(X_test)
# 평가 지표 계산: 정확도 (맞은수/전체)
acc_train = accuracy_score(y_train, y_train_pred_svm)
acc_test = accuracy_score(y_test, y_test_pred_svm)
print(f'학습 데이터를 이용한 SVM Acc 값 : {acc_train*100:.1f}%')
print(f'평가 데이터를 이용한 SVM Acc 값 : {acc_test*100:.1f}%')
► 로지스틱 회귀 모델을 사용했을 때 평가 데이터를 활용한 정확도가 82.9% 였던것에 비하면 성능이 매우 향상된 것을 알 수 있다.
# confusion matrix을 활용한 평가 결과 확인
cm_test_svm = confusion_matrix(y_test, y_test_pred_svm)
plt.imshow(cm_test_svm, interpolation='nearest', cmap='Blues')
plt.title("SVM Confusion Matrix (Test)")
plt.colorbar()
tick_marks = np.arange(len(np.unique(y_test)))
plt.xticks(tick_marks, np.unique(y_test))
plt.yticks(tick_marks, np.unique(y_test))
plt.xlabel("Predicted Label")
plt.ylabel("True Label")
# 각 셀에 숫자 표시
for i in range(cm_test_svm.shape[0]):
for j in range(cm_test_svm.shape[1]):
plt.text(j, i, cm_test_svm[i, j], ha="center", va="center", color="black")
# 정밀도, 재현율, F1 값 비교
from sklearn.metrics import precision_score, recall_score, f1_score
logistic_precision = precision_score(y_test, y_test_pred_logis)
logistic_recall = recall_score(y_test, y_test_pred_logis)
logistic_f1 = f1_score(y_test, y_test_pred_logis)
print(f'Logistic의 P,R,F1 : {logistic_precision:.2f} / {logistic_recall:.2f} / {logistic_f1:.2f}')
svm_precision = precision_score(y_test, y_test_pred_svm)
svm_recall = recall_score(y_test, y_test_pred_svm)
svm_f1 = f1_score(y_test, y_test_pred_svm)
print(f'SVM의 P,R,F1 : {svm_precision:.2f} / {svm_recall:.2f} / {svm_f1:.2f}')
► 로지스틱 회귀보다 SVM 모델을 활용한 예측이 훨씬 더 정확하다고 해석할 수 있다.
※ 분류 평가 척도 - 정밀도 / 재현율 / F1 점수
1. 정밀도 (Precision)
- 예측한 양성 결과가 실제로 얼마나 진짜 양성인지를 계산
- 모델이 양성 결과를 잘 찾아내야 하는 상황에서 중요
2. 재현율 (Recall)
- 실제 양성 중 얼마나 양성을 잘 찾아냈는지를 계산
- 정답을 잘 찾아내는 과정에서 중요
※ 정밀도와 재현율은 서로 Trade-off 관계
'(엄청 신중하게)이것은 정답일 수 밖에 없다.' 라고 판단한 것들만 양성이라고 얘기하면 정밀도는 늘어난다.
반면, 재현율은 떨어진다. (∵ 딱 봐도 정답인데 정답이라고 안하고 신중하게 판단 후에 정답이라고 하니까)
3. F1 Score
- 정밀도와 재현율의 조화 평균
- 조화평균을 사용해 낮음 점수에 대한 패널티를 늘림
- 정밀도와 재현율이 전반적으로 좋아야 좋은 F1값을 갖을 수 있음
Decision Tree를 활용한 풀이
- 엔트로피 결정 경계 사용
- 트리의 최대 깊이
max_depth = 5로 설정 - SVM에 비해 학습 속도가 빠름 (트리 깊이에 따라 변동성이 크긴함)
- DT의 시간 복잡도 :
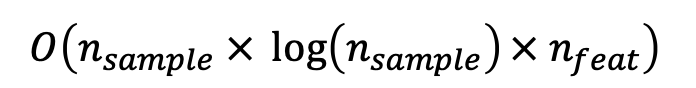
1단계. Decision Tree 모델을 활용한 학습
from sklearn.tree import DecisionTreeClassifier
dt = DecisionTreeClassifier(criterion='entropy',
max_depth=5,
min_samples_split=5)
%%timeit
dt.fit(X_train, y_train)
from sklearn.tree import plot_tree
plt.figure(figsize=(100, 20))
plot_tree(dt, filled=True,
feature_names=ext_ordinal_columns + ext_category_columns,
class_names=['satisfied', 'unsatisfied'])
plt.title("Plot of Decision Tree")
plt.show()
머신 러닝 모델의 크기가 커지고 복잡도가 증가하면 모델의 성능은 올라간다.
하지만, 과적합이 발생하며 오히려 성능이 하락하기도 한다.
∴ 평가 데이터에 대한 성능이 낮아지기 시작하는 지점의 세팅을 이용해 최적의 모델을 선택하는 것이 바람직하다
2단계. max_depth를 조절하면서 최적의 모델 찾기
# max depth에 따른 학습 결과 경향성 파악
max_depths = range(3, 30)
# 훈련 데이터 정확도와 테스트 데이터 정확도를 각각 빈 리스트로 만들고
# for문을 3부터 30까지 돌면서 최고의 모델을 찾는 방식으로 알고리즘 작성
train_accuracies = []
test_accuracies = []
for depth in max_depths:
model = DecisionTreeClassifier(criterion='entropy',
max_depth=depth,
min_samples_split=5)
model.fit(X_train, y_train)
# 학습 데이터에 대한 정확도
y_train_pred = model.predict(X_train)
train_acc = accuracy_score(y_train, y_train_pred)
train_accuracies.append(train_acc)
# 평가 데이터에 대한 정확도
y_test_pred = model.predict(X_test)
test_acc = accuracy_score(y_test, y_test_pred)
test_accuracies.append(test_acc)
# 결과 시각화
plt.figure(figsize=(10, 6))
plt.plot(max_depths, train_accuracies, label='Training Accuracy')
plt.plot(max_depths, test_accuracies, label='Test Accuracy')
plt.xlabel('Max Depth')
plt.ylabel('Accuracy')
plt.title('Decision Tree Accuracy vs Max Depth')
plt.legend()
plt.show()
# 최대 정확도를 달성하는 max_depth를 찾고 해당 depth로 최적 모델 학습
max_acc = max(test_accuracies)
best_depth = max_depths[test_accuracies.index(max_acc)]
print('최대 정확도의 depth :', best_depth)
dt = DecisionTreeClassifier(criterion='entropy',
max_depth=best_depth,
min_samples_split=5)
# 예측 수행
y_train_pred_dt = dt.predict(X_train)
y_test_pred_dt = dt.predict(X_test)
# 평가 지표 계산: 정확도 (맞은수/전체)
acc_train = accuracy_score(y_train, y_train_pred_dt)
acc_test = accuracy_score(y_test, y_test_pred_dt)
print(f'학습 데이터를 이용한 DT Acc 값 : {acc_train*100:.1f}%')
print(f'평가 데이터를 이용한 DT Acc 값 : {acc_test*100:.1f}%')
► 최적의 max_depth = 16 인 것을 찾고 이를 모델에 적용 시킨 결과, 정확도가 확연히 높아진 것을 알 수 있다.
# confusion matrix을 활용한 평가 결과 확인
cm_test_dt = confusion_matrix(y_test, y_test_pred_dt)
plt.imshow(cm_test_dt, interpolation='nearest', cmap='Blues')
plt.title("Decision Tree Confusion Matrix (Test)")
plt.colorbar()
tick_marks = np.arange(len(np.unique(y_test)))
plt.xticks(tick_marks, np.unique(y_test))
plt.yticks(tick_marks, np.unique(y_test))
plt.xlabel("Predicted Label")
plt.ylabel("True Label")
# 각 셀에 숫자 표시
for i in range(cm_test_dt.shape[0]):
for j in range(cm_test_dt.shape[1]):
plt.text(j, i, cm_test_dt[i, j], ha="center", va="center", color="black")
3단계. 각각 로지스틱, SVM, DT를 활용했을 때의 성능 비교해보기
# 정밀도, 재현율, F1 값 비교
from sklearn.metrics import precision_score, recall_score, f1_score
logistic_precision = precision_score(y_test, y_test_pred_logis)
logistic_recall = recall_score(y_test, y_test_pred_logis)
logistic_f1 = f1_score(y_test, y_test_pred_logis)
print(f'Logistic의 P,R,F1 : {logistic_precision:.2f} / {logistic_recall:.2f} / {logistic_f1:.2f}')
svm_precision = precision_score(y_test, y_test_pred_svm)
svm_recall = recall_score(y_test, y_test_pred_svm)
svm_f1 = f1_score(y_test, y_test_pred_svm)
print(f'SVM의 P,R,F1 : {svm_precision:.2f} / {svm_recall:.2f} / {svm_f1:.2f}')
dt_precision = precision_score(y_test, y_test_pred_dt)
dt_recall = recall_score(y_test, y_test_pred_dt)
dt_f1 = f1_score(y_test, y_test_pred_dt)
print(f'DT의 P,R,F1 : {dt_precision:.2f} / {dt_recall:.2f} / {dt_f1:.2f}')
