Decision Tree (의사결정나무)
: 데이터를 잘 나누기 위한 결정 경계를 찾는 것을 목표로 함
DT 용어

노드
- 데이터에 대한 특정 질문이나 조건
- 데이터를 분류하는 과정에서 사용
엣지
- 노드와 노드를 연결하는 선
- 상위노드의 특정 질문에 대한 가능한 답변
루트 노드
- 트리의 가장 상단에 위치한 노드
- 분류(혹은 예측)를 시작하는 지점
분할 노드(결정 노드)
- 데이터를 더 작은 하위 집합으로 나누는데 사용되는 중간 노드
리프 노드(터미널 노드)
- 트리의 가장 말단에 위치한 노드
- 분기와 자식노드를 갖지 않음
결정 기준(Decision Criteria)
: 데이터를 분할하는 기준을 결정하는데 사용되는 방법론
- 트리의 깊이와 복잡성 관리 가능
- 좋은 결정 기준 → 트리를 간결/효율적으로 만듦 → 과적합 방지, 일반화 성능 향상
- 분류 과정에서 사용되는 결정 기준 :
- 정보 이득
- 지니 불순도
- 회귀 과정에서 사용되는 결정 기준 :
- MSE 최소화
분류 문제를 위한 결정 기준
1. 엔트로피 (Entropy)
: 어떤 상황 or 현상이 갖고 있는 불확실성
- 포함하는 정보량과 반비례


Decision Tree에서 엔트로피의 역할
- 각 상황은 특정한 정도의 엔트로피를 갖고 있음
► 각 노드에 포함되는 데이터의 순도(=클래스)에 따라 엔트로피가 계산됨
- 노드 안에 서로 다른 클래스의 데이터가 많이 섞여있으면 : 순도↓
- 같은 클래스의 데이터가 모여 있다면 : 순도↑
정보 이득(Information Gain)
: 부모 노드와 자식 노드들의 엔트로피를 계산하여 엔트로피가 낮아지는 방향(=순도가 높아지는 방향)으로 결정 경계를 선정하는 것
= 정보 이득을 최대화 하는 방향

엔트로피 활용 DT 모델 생성 실습
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
seed = 1234
np.random.seed(seed)
# 데이터 생성
X, y = make_classification(n_samples=100,
n_features=2,
n_informative=2, # 생성할 데이터셋에서 유의미한 특성의 수
n_redundant=0,
n_clusters_per_class=1,
n_classes=3, # 생성할 데이터셋의 타겟 클래스의 수
random_state=1)
# 데이터셋을 훈련 세트와 테스트 세트로 분할
X, X_test, y, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 데이터 시각화
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
plt.xlabel('feature1')
plt.ylabel('featuer2')
plt.margins(0.2)
plt.show()
# 정보 이득을 사용하는 결정 트리 분류기 생성
dt_entropy = DecisionTreeClassifier(criterion='entropy',
max_depth=3,
min_samples_split=3) # 분기 진행 시작 조건인 노드 내 샘플 수(=적어도 3개 이상 있어야 데이터 분리하겠다)
dt_entropy.fit(X, y)# 두 모델의 훈련된 구조를 확인
from sklearn.tree import plot_tree
# 정보 이득을 사용한 결정 트리
plt.figure(figsize=(24, 12))
plot_tree(dt_entropy, filled=True,
feature_names=['Feature 1', 'Feature 2'],
class_names=['Class 0', 'Class 1', 'Class 2'])
plt.title("Decision Tree using Entropy")
plt.show()
2. 지니 불순도 (Gini Impurity)
: 데이터 내 클래스 분포의 불균형을 평가하는 방법


지니 불순도 활용 DT 모델 생성 실습
# 지니 불순도를 사용하는 결정 트리 분류기 생성
dt_gini = DecisionTreeClassifier(criterion='gini',
max_depth=3, # 만들 트리가 얼만큼 깊은지(1개만 있으면 0)
min_samples_split=3) # 분기 진행 시작 조건인 노드 내 샘플 수
dt_gini.fit(X, y)# 지니 불순도를 사용한 결정 트리
plt.figure(figsize=(24, 12))
plot_tree(dt_gini, filled=True,
feature_names=['Feature 1', 'Feature 2'],
class_names=['Class 0', 'Class 1', 'Class 2'])
plt.title("Decision Tree using Gini")
plt.show()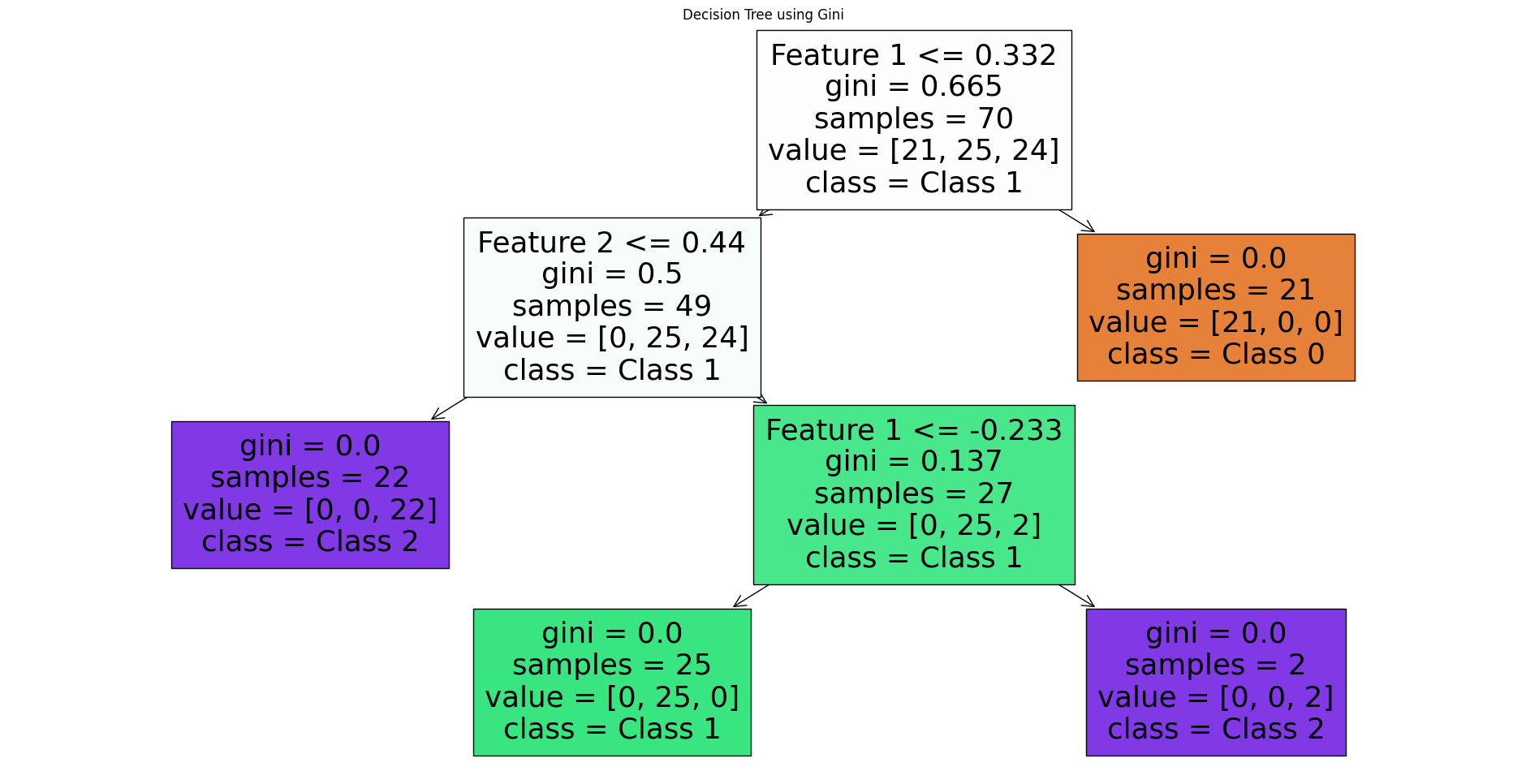
# 결정 경계 그려보기
import numpy as np
# 데이터와 결정 경계를 시각화하는 함수
def plot_decision_boundaries(X, y, model, title):
# 마커와 색상 설정
markers = ('s', 'x', 'o')
colors = ('red', 'blue', 'green')
cmap = plt.cm.RdYlBu
# 결정 경계 그리기
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.01),
np.arange(x2_min, x2_max, 0.01))
Z = model.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
# 데이터셋의 샘플 플로팅
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
alpha=0.8, c=colors[idx],
marker=markers[idx], label=f'Class {cl}')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(loc='upper left')
plt.title(title)
# 첫 번째 특성과 두 번째 특성을 이용한 데이터셋 시각화
plt.figure(figsize=(24, 12))
plt.subplot(1, 2, 1)
plot_decision_boundaries(X, y, dt_entropy, "Decision Tree (Entropy)")
plt.subplot(1, 2, 2)
plot_decision_boundaries(X, y, dt_gini, "Decision Tree (Gini)")
plt.show()
회귀 문제를 위한 결정 기준
3. MSE 최소화
: 각 노드에서 실제 정답과 예측값 사이의 평균 제곱 오차(MSE)의 평균을 계산하고 이 값을 최소화하는 노드를 찾아가는 방식으로 트리가 만들어짐
MSE 최소화 활용 DT 생성 실습
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
# 데이터 생성 변수
w0 = 2.3
w1 = 1
num_data = 100
noise = np.random.normal(0, 3, num_data)
# 데이터 생성
X = np.linspace(0, 5, num_data)
y = w0 + w1 * (X ** 2) + noise
# 시각화
plt.scatter(X, y)
plt.xlabel('X')
plt.ylabel('y')
plt.margins(0.2)
plt.show()
X = X.reshape(-1, 1) # 학습을 위한 차원 변환 진행
# MSE 최소화 결정 트리 생성
dt_mse_reg = DecisionTreeRegressor(max_depth=3) # 2^3=8개의 계단 형태로 만들어짐
dt_mse_reg.fit(X, y)# 트리 시각화
plt.figure(figsize=(24, 12))
plot_tree(dt_mse_reg, filled=True,
feature_names=['Feature 1', 'Feature 2'])
plt.title("Decision Tree using MSE")
plt.show()
# 결과 예측 진행
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_pred = dt_mse_reg.predict(X_test)
# 시각화
plt.figure(figsize=(10, 6))
plt.scatter(X, y,
s=20, edgecolor="black",
c="darkorange", label="data")
plt.plot(X_test, y_pred,
color="cornflowerblue", label="prediction", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()
DT 사용시 주의할 점
- 축에 수직인 방향으로 데이터가 분할됨
- 따라서 축에 수직한 데이터는 쉽게 해결하지만, 경계면이 회전이 되어있다면 구불구불한 경계면이 생성됨
- 일반화에 어려움이 있을 수 있음
- 필요시 주성분 분석(PCA)을통한 데이터 회전이 필요할 수 있음
- 데이터 노이즈에 굉장히 민감하며
- 특정 데이터의 추가가 전체 모델 결과에 큰 변화를 줄 수 있음
- Outlier 처리, 전처리를 필수로 해줘야 함
- Depth가 깊다면 과적합 위험이 큼 (보통 `max_depth = 3`으로 설정함)
