선형 관계
: 독립 변수가 파라미터 값 만큼 일정한 비율로 결과 종속 변수에 영향을 미치는 관계
마트에서 과자(단가 1500원)와 우유(1200원)를 사는 것을 가정해보자.

- [조건] 물건 가격 할인과 서로 다른 물건 끼리의 가격 영향은 없음
- 전체 비용은 구매하는 과자와 우유 수에 영향을 받음
- 독립 변수 : num_과자, num_우유
- 파라미터 : 1500원(price_과자), 1200원(price_우유)
- 종속 변수 : TotalCost
선형 결합
: 파라미터들이 어떠한 실수(혹은 벡터)와 가중합(곱하기&더하기)으로 표현된 것

- 𝑥1 ... 𝑥n : 독립 변수 혹은 특징(feature) ► 입력하는 데이터
- 𝑤1 ...𝑤n : 파라미터 ► 찾아 내야 하는 값
선형 모델
: 파라미터들이 선형 결합을 이루고, 이것으로 종속변수의 값을 표현할 수 있을 때의 식(모델)

- y : 종속변수
→ 이 선형 모델을 그래프로 표현한다면 직선(in 2D) 혹은 평면(in 3D) 혹은 초평면(Hyper-plane, over 4D)이라고 함
"선형 모델을 학습한다"
= 종속변수가 어떠한 값을 갖게 하기 위해, 특정 제약 조건이 주어진 상태에서 적절한 파라미터 값을 찾는 것
(상태 : Loss를 줄이는 최적의 상태 or 성능이 제일 높아지는 상태 등)
선형 vs. 비선형
선형과 비선형을 구분하는 큰 기준은 "종속변수가 파라미터에 대해 선형적인지 or 비선형적인지"에 따라 다름
∴ 일단 파라미터가 종속변수에 미치는 영향이 "선형적이다." 라는 가정으로 선형 모델을 사용한다.
선형 모델의 가정
: 서로 다른 독립 변수는 서로 상관성이 없어야 한다.
- 만약 두 독립변수 사이에 높은 상관관계(correlation)이 존재한다면, 다중공선성(multicollinearity) 문제를 일으킴
→ 정확도 및 신뢰성 저하
→ 해석력에 복잡성 증가
선형 회귀
"선형 회귀 모델을 사용한다."
= 입력 데이터 특징 사이의 독립성을 가정하고 데이터 특징에 대한 선형 결합으로 회귀 문제를 풀겠다.

- ŷ : 예측값 (출력 결과)
-
𝑤0 : 절편(혹은 편향)
- 데이터(x)에 관계 없이 결괏값(y hat)에 직접적으로 영향을 미치는 값
- 목푯값의 평균이 0에 맞춰져 있다면 절편을 추가하지 않을 수 있음
- 일반적으로는 절편을 포함하는 것이 유리함
- 가중합(덧셈&곱셈)으로 표현되는 다항식은 행렬곱(𝑋𝑤)으로 간단하게 표현할 수 있음
비용 함수 (= 평균 제곱 오차; Mean Squared Error)
비용 : 정답과 예측이 다른 것
w 값에 따라 모델이 좋은지 나쁜지를 결정한다.
모델이 좋은지 나쁜지에 따라 비용 함수의 크기가 달라진다.
w 값이 좋으면 J가 작아지고, w값이 나쁘면 J가 커진다.
즉, J가 낮아지는 방향으로 문제를 풀어야 함
최적화 (Optimization)
: 특정 문제에서 최적의 해를 찾는 과정
최적
: 특정 함수의 최솟값(min) 혹은 최댓값(max)를 찾는 것
선형 회귀 문제를 위한 최적화 방법론
아래 두 방법 모두 같은 해를 제공하지만,
선형 모델의 가장 큰 가정인 독립 변수 간의 강한 상관 관계가 있다면(=독립성이 깨진다면), 다중 공선성 문제가 발생할 수 있다.
데이터의 상황에 맞게 적절히 선택해서 사용 가능
1. 정규 방정식 풀이
- 파라미터 값을 직접 계산하는 방법
- 최솟값을 찾기 위해 도합수f'(x) = 0되는 점 x를 계산하는 것
- 튜닝할 변수가 없이 명시적으로 해를 제공
- 하지만 특성의 수가 많다면 계산 복잡도와 메모리가 많이 필요
- 따라서 훈련세트가 크지 않은 상황에서 빠르게 해를 구하기 좋음
n(데이터의 개수)에 독립적
→ 일반적으로 𝑛≫𝑝 인 경우 (입력데이터≫특성의수)에 유용함
2. 경사 하강법 (Gradient Decent)
: 비용 함수가 작아지는 방향을 찾아 점진적으로 반복해서 파라미터를 조정하는 방법

- 임의로 잡은 초기 파라미터 값(w)을 기준으로 비용 함수의 기울기를 계산하여 기울기가 줄어드는 방향으로 파라미터를 수정 이동
→ 반복 수행으로 기울기가 0에 가까워지면(=최적값에 도달하면) 멈춤 - 특성 수와 샘플의 수에 민감도가 적음
- 변수 튜닝(ex. 학습률, 학습량)이 결과에 영향을 줄 수 있음
- 주의 사항 : 적절한 학습률에 대한 탐구가 필요함
- 값이 너무 작다면 : 최적화 소요 시간 증가
- 값이 너무 크다면 : 발산 or 최적화 도달 가능성 감소
학습률(Learning Rate)
: 얼마나 빠르게 내려갈 것인지(학습 속도)
✓ 파라미터 업데이트
1. 비용함수(𝐽(𝑤))를 통해 구한 전체 비용을 대상으로

2. 각 파라미터의 미분값(w에 대한 편미분)을 구하고

3. 현재 값을 기준으로 기울기가 작아지는 방향으로 이동함으로써 새로운 w를 업데이트한다.
이때, 너무 빠른 or 느린 학습을 방지하기 위해 적절한 학습률(lr)이 사용된다.

✓ 확률적 경사 하강법 (Stochastic Gradient Decent)
기존의 경사 하강법은 모든 학습 데이터에 대해 기울기 계산을 진행하므로 학습 데이터가 많은 경우(𝑛 ≫𝑝) 소요 시간이 기하 급수적으로 증가
► 이를 극복하기 위해, 전체 데이터 중 임의로 일부 데이터를 샘플링하여 그것을 대상으로 경사 하강법을 진행하는 '확률적 경사 하강법'을 사용

- 작은 데이터로 수정 이동을 반복하므로 빠른 수렴 가능
- 데이터가 많거나(𝑛 ≫) 특성 feature가 많은 경우(𝑝 ≫) 사용하기 용이함
다중공선성 (Multicollinearity)
: 입력 데이터가 갖는 특징값들 사이에 강력한 상관관계가 존재할 때 발생하는 문제
- 머신러닝 모델이 작은 데이터 변화에도 민감하게 반응
- 안정성과 해석력을 저하시킴
- 다중 공선성이 있는 데이터 사용 시, 정규 방정식으로 해를 구하는 상황에서 문제 발생
- 정규 방정식 해 풀이에 사용되는 역행렬이 존재하지 않을 수 있음
-
𝑋^T*𝑋 의 값이 점차 특이 행렬(Singular matrix)에 가까워짐
► w를 구할 수 없게 됨
특이 행렬(Singular Matrix)
: 역행렬을 구할 수 없는 행렬
► 강한 다중공선성이 있는 경우 정규 방정식으로 풀 수 없는 해를 다른 방식으로 구하는 방법인 SVD-OLS(회피 방법)사용
SVD-OLS (Singular Value Decomposition-OLS)
: SVD(특이값 분해)를 활용해서 선형 회귀 모델의 해를 구하는 방법
- 시간복잡도 : 𝑂(𝑛𝑝^2)
- 𝑛 : 입력데이터 수
- 𝑝 : 사용하는 특성의 수
- 풀이 과정 :
1. 학습 데이터를 모아둔 행렬 X에 SVD를 적용시켜 특이값을 분해

2. 특이값이 분해된 입력 X에 OLS(정규 방정식 풀이)방식의 풀이를 적용

3. 변경한 식을 바탕으로 해를 구함

로지스틱 회귀(Logistic Regression)
: 이진 분류 문제를 해결하기 위한 기본 알고리즘 중 하나로, 입력 데이터가 후보 클래스 중 각각의 클래스일 확률을 예측하는 모델
[문제] 이진 분류
: A인가? B인가?
[해결을 위해 사용되는 알고리즘] 로지스틱 회귀
: A 클래스일 확률이 60%인가? B 클래스일 확률이 40%인가?
- 확률을 직접적으로 예측(=확률 추정)하는 방식으로 문제 해결
- 확률이므로 값의 범위 = 0 ~ 1 사이 실수값
- 분류 문제를 풀기 위해 회귀 방식으로 문제를 접근하는 것
- 예측한 특정 클래스의 확률 값이
- (일반적으로) 50% 이상 = 해당 클래스에 속한다고 예측 = 양성(positive)
- 50% 미만 = 해당 클래스에 속하지 않는다고 예측 = 음성(negative)
- 로지스틱 회귀도 선형 모델의 조건(독립 변수간 독립성)을 가정한다.


✓ 로짓 logit (=로그 오즈 log-odds)
- 오즈(odds) : 특정 사건이 발생할 확률(𝑝)과 발생하지 않을 확률(1 − 𝑝)의 비율

- 로그 오즈(log-odds) : 오즈에 로그 함수를 씌운 것 (±∞의 범위를 갖음)

✓ 로지스틱 함수 Logistic-function (=시그모이드 Sigmoid)
: 로그 오즈의 역함수로, 로짓(logit)을 입력으로 주면 확률 𝑝를 반환
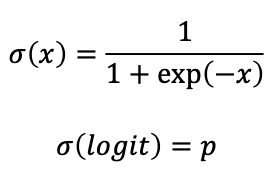
- 출력은 항상 0~1사이의 값
- 함수의 개형이 S자 모양

[정리]
► 선형 회귀 식을 p를 구하는 것이 아니라 logit을 구하도록 변환해서 나온 결과를 갖고 역으로 p를 구하는 방식
► 로지스틱 회귀 모델의 출력 결과 = 로짓(로그 오즈)
즉, 특정 클래스일 확률(p)를 알기 위해 로지스틱 함수를 활용하는 것
비용 함수
◆ 다중 클래스 분류 문제의 경우 접근법
1. One-vs-One(OvO)
: 각각의 클래스 하나 하나를 비교하는 방법
ex) A, B, C의 클래스가 있다고 가정해보자.
► A vs. B를 구분하는 모델, B vs. C를 구분하는 모델, C vs. A를 구분하는 모델 3개를 만들어서 확률 추정값을 각각 비교한다.
2. One-vs-Rest(OvR)
: 각 클래스가 맞는지 아닌지를 비교하는 방법
ex) A, B, C의 클래스가 있다고 가정해보자.
► A인지 아닌지를 구분하는 모델, B인지 아닌지를 구분하는 모델, C인지 아닌지를 구분하는 모델 3개를 만들어서 확률 추정값을 각각 비교한다.
3. Softmax Regression
: 각 클래스의 확률 추정값 중 가장 큰 것으로 예측하는 방법
ex) A, B, C의 클래스가 있다고 가정해보자.
►A, B, C 각각의 확률을 추정해서 가장 큰 확률을 갖는 것으로 예측한다.
