📌 학습목표
1. 선형대수
2. 확률 분포
3. 확률론적 모델링과 추론
선형대수
: 수 들이 모여있는(=벡터 or 행렬) 개념과 관련된 식을 연구하는 수학의 한 분야로,
수를 다루는 많은 학문(데이터, 공학, 과학적 분석 등)에서 수의 연산을 빠르고 효과적으로 하기 위해 사용하는 도구
- 수의 집합을 기하학적인 형상으로 적용하여 표현
- 시각적이고 직관적으로 수의 값을 이해할 수 있음
- 기하학적으로 의미를 갖는 다양한 변환을 수학적으로 정의할 수 있음(ex. 회전, 스케일링 등)
- 컴퓨터 그래픽스, 엔지니어링, 물리학, 컴퓨터 과학, 머신러닝 등 다양한 분야에서 응용
- 머신러닝에서는 데이터를 표현하고 변환하는데 필수적인 도구로 사용됨
◆ 수의 집합 : {스칼라, 벡터, 행렬, 텐서}
숫자는 특정한 방향(=차원)으로 줄을 서듯 모일 수 있음
(※ 숫자들이 얼마나 모이는지에 따라 크기가 정해진다.)
► 데이터를 벡터 or 행렬의 형태로 변환이 가능하며, 이에 익숙해지면 데이터를 다루는 데 용이해진다!

- 스칼라 : 다른 숫자와 함께하지 않고 홀로 존재하는 수
- 벡터 : 한쪽 방향(차원)으로만 숫자가 모인 형태> 1차원
- 행렬 : 두 방향으로 숫자가 줄을 선 형태 >2차원
- 텐서 : 벡터와 행렬을 일반화한 개념.
- 0차원 텐서 = 스칼라
- 1차원 텐서 = 벡터
- 2차원 텐서 = 행렬
- 3차원 이상의 수 집합을 나타내는 용어이기도 함
◆ 행렬의 연산
1) 행렬의 덧셈과 뺄셈
- 같은 크기의 행렬끼리만 가능
- 각 행렬의 같은 자리에 있는 원소끼리의 덧셈과 뺄셈(element-wise operation)을 수행하는 것
2) 행렬의 곱셈
- 하나의 행렬의 각 행과 다른 행렬의 각 열 간의 내적(=벡터 간의 연산)
- 두 벡터의 동일한 위치에 있는 원소를 곱한 후, 그 결과를 모두 더하는 연산 (결과는 스칼라)
- Element-wise 연산이 아니므로 행렬의 크기가 달라도 연산이 가능
(※ 대신, 앞선 행렬의 열과 뒷 행렬의 행의 크기가 같아야 함)
3) 전치행렬 (Transpose)
- 하나의 행렬이 주어질 때, 행과 열을 바꾼 행렬
- A행렬의 크기가 m X n 이라면 A 행렬의 전치 행렬은 A^T 으로 표기하고, 그것의 크기는 n X m 이 됨
- 대각선 원소는 전치 과정에서 그대로 유지됨
- 대칭 행렬 : A= A^T 인 경우
- 곱셈의 경우 순서가 바뀜 : (AB)^T = B^T*A^T
4) 역행렬 (Inverse Matrix)
- 특정 행렬 A에 어떤 행렬 B를 곱해보니 결과가 항등 행렬이라면, B를 A의 역행렬이라고 한다.
- 모든 행렬이 역행렬을 갖는것은 아님
- A 행렬이 역행렬을 가지려면, A는 반드시 가역(또는 비특이, non-singular) 해야 함
- 이를 수학적으로 표현하면 det(A) ≠ 0을 만족해야 함
- 방정식을 비유적으로 생각하면 ax= 1을 만족하는 x를 찾고자 한다면 a ≠ 0 이 아니어야 함!
- '가역적' = 원래 상태(1)로 돌릴 수 있음
- 다음의 성질을 갖는다 :

◆ 선형 변환 (Linear Transformation)
: 벡터의 방향과 크기의 변경
어떤 벡터(v)에 대해서 v는 벡터 크기 만큼의 차원 공간에 존재한다고 하자.
여기에 특정 행렬(A)를 곱해서 새로운 벡터 (v')을 만들었다고 가정했을 때,
- v와 v'는 A 행렬에 의해 방향이 바뀜
- 예를 들어 :

- 특정 벡터에 어떠한 행렬을 곱하면 벡터의 방향 혹은 크기가 변경

◆ 고유벡터(Eigenvector)와 고유값(Eigenvalue)
이번에는 특정 행렬 (A)의 입장에서 보자.
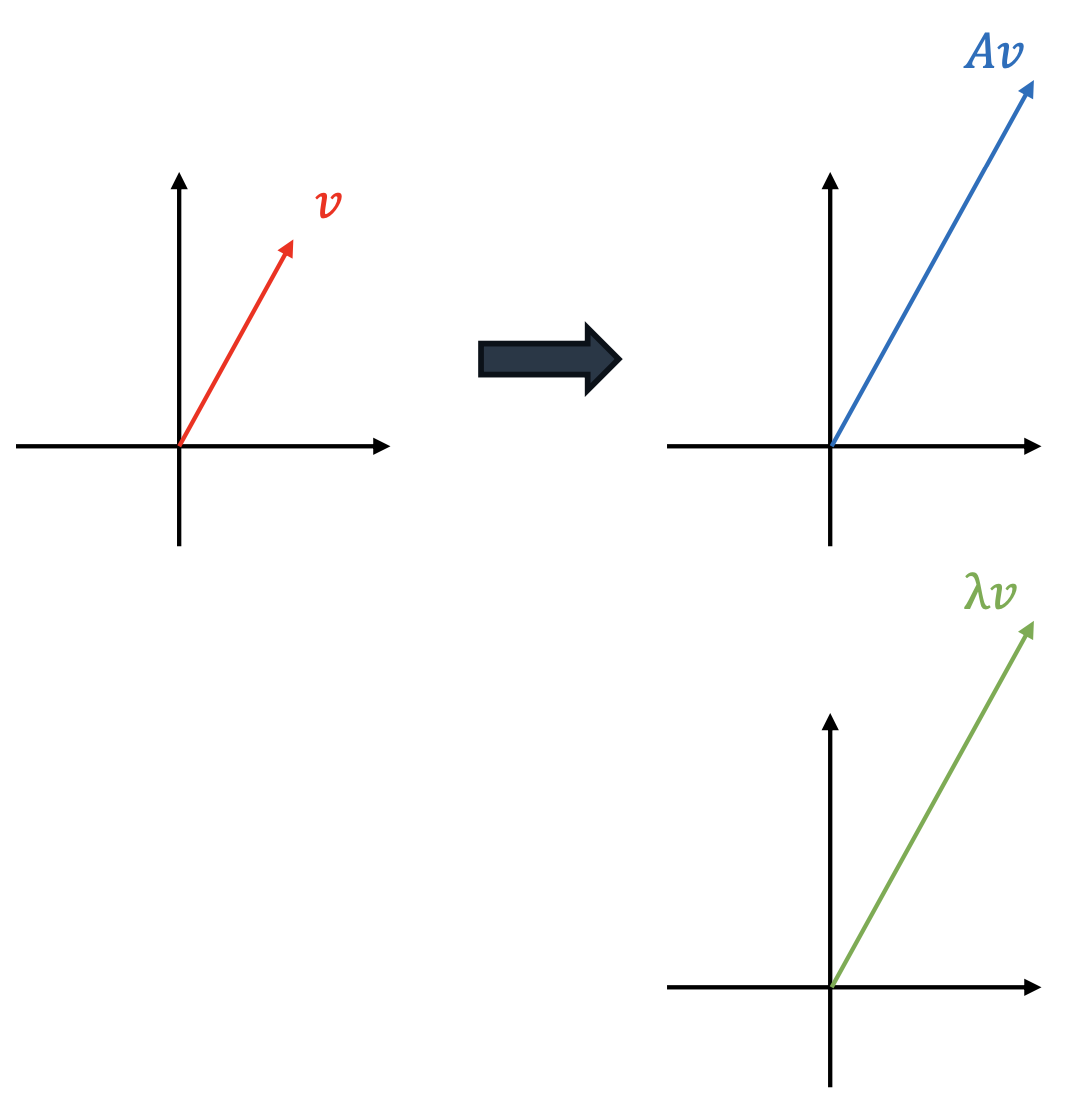
행렬 A에는 다양한 벡터를 곱할 수 있고, 𝐴𝑣 = 𝜆𝑣 (𝜆 : 임의의상수) 와 같은 특징을 갖는 벡터가 존재할 수 있음
- 𝐴𝑣 = 𝜆𝑣 : 𝐴행렬에 임의의 벡터 𝑣를 곱하니, 그결과가 벡터 𝑣의 크기를 상수 𝜆배 한 벡터와 같다
- 𝑣 : 고유벡터(Eigenvector)
- 상수 𝜆 : 고유값(Eigenvalue)
◆ 데이터 분석에서 사용되는 방식
- 행렬 𝐴의 고유벡터 : 행렬 𝐴의 값이 가장 많이 분산되는 방향을 나타냄
- 분산이 많이 된다는 것은 = 많은 정보력을 갖고 있다
- 일반적으로 데이터를 불러오면 행렬의 형태를 갖게 됨
- 이 데이터를 담아온 행렬을 𝐴라고 보면, 데이터가 담고있는 여러 정보 중 가장 의미가 큰 방향이 '고유벡터 𝑣'가 됨
- 해당 방향으로 얼만큼 분산이 이루어졌는지 분산의 크기를 나타내는 정도가 고유값 𝜆
- 이러한 고유벡터와 고유값은 복수개가 가능하며 고유값을 기준으로 나열된 고유벡터는 해석력이 큰 방향의 순서를 의미함
- 이 둘은 데이터를 이해하고 계산하는 과정에서 사용됨
- 의미를 유지한 상태로 데이터를 전처리
- 행렬 계산을 간소화

◆ 특이값 분해 (Singular Value Decomposition; SVD)
: 복잡한 행렬 𝐴 (𝑚×𝑛)을 더 간단한 세 가지 행렬(𝑈,Σ,𝑉")로 분해하는 과정
- 𝐴=𝑈Σ𝑉"
- 𝑈의 열벡터들은 𝐴의 왼쪽 특이벡터로 𝐴𝐴"의 고유벡터
- 𝑉의 열벡터들은 𝐴의 오른쪽 특이벡터로 𝐴"𝐴의 고유벡터
- Σ의 대각선 위의 값들로 𝐴의 특이값 : 원래 행렬 𝐴의 데이터가 가진 중요도를 의미
◆ 고유벡터, 고유값, SVD의 관계
: 모두 행렬 A에서 정보를 추출하는 과정
► SVD가 조금 더 일반적인 경우를 나타내며, 고유벡터와 고유값은 SVD의 스페셜 케이스로 보면 됨
- 고유벡터 & 고유값 분석 : 행렬 𝐴가 정사각 행렬일 경우에 사용 가능
- SVD : 직사각 행렬 𝐴에 대해 사용 가능

- 𝐴행렬의 크기가 (𝑚×𝑛)이라고 할 때, 정사각행렬이 아니므로 바로 고유벡터와 고유값분석을 할 수 없음
→ 행렬 𝐴에서 행과 열 방향으로 나눠 따로 행 사이의 관계와 열 사이의 관계를 보고자 함 - 𝐴𝐴"는 (𝑚×𝑚)의 크기를 갖고 있어 고유벡터와 고유값 분석이 가능
- 𝐴𝐴"는 원래 행렬 𝐴의 행 사이의 관계도가 데이터의 형태로 존재하며 그들의 정보력 중, 분산이 크고 중요한 의미를 갖는 방향벡터가 𝑈행렬 안에 정리될 것
- 𝐴"𝐴도 마찬가지
- 단, 원본행렬𝐴의 열 사이의 관계를 바탕으로 고유값 및 고유벡터 분석 진행
- 𝐴𝐴" 혹은 𝐴"𝐴의 고유값의 제곱근 값을 𝐴의 특이값 이라고함
- 𝐴𝐴" 의 고유값과 𝐴"𝐴의 고유값은 서로 같음
- Σ행렬은 𝐴의 특이값을 대각선 위치에 갖고 있고, 대각선을 제외한 나머지 모든 값은 0
- 고유값 분석과 마찬가지로 행렬 𝐴의 선형 변환에서 중요한 스케일링 정보를 포함하고 있음
𝒎×𝒏 크기를 갖는 행렬 𝑨는 𝐴 = 𝑈Σ𝑉'
𝑼(왼쪽 특이 벡터들)
• 크기 : 𝑚×𝑚
• 원본행렬 𝐴의 행 정보를 바탕으로 중요도를 파악
𝑽 (오른쪽 특이 벡터들)
• 크기 : 𝑛×𝑛
• 원본행렬 𝐴의 열 정보를 바탕으로 중요도를 파악
𝜮 (특이값들)
• 크기 : 𝑚×𝑛
• 행렬 𝐴 선형 변환 과정에서 영향을 미치는 스케일링 정보(특이값)를 포함
확률 분포
◆ 확률 (Probability)
: 특정한 사건이 일어날 가능성을 수치로 표현한 것으로 0~1 사이의 값을 갖는다. (0 ≤ P ≤ 1)
- 일반적으로 확률(Probability)의 P를 활용해 확률을 표시
- 어떠한 사건인지 사건을 알려주는 확률 변수(probability variable) x를 활용
- 𝑃(𝑥) :확률변수 x가 특정 값을 가질 확률
- 기본적인 확률 연산
- 합의 법칙 : 두사건 A와 B가 서로 베타적(두 사건이 동시에 발생하지 X)이라면, A 또는 B 확률
→ 𝑃(𝐴) + 𝑃(𝐵) - 곱의 법칙 : 두사건 A와 B가 서로 독립(하나의 사건이 다른 사건에 영향을 주지 X)일 때, A와 B가 동시에 발생할 확률
→ 𝑃(𝐴) × 𝑃(𝐵) - 조건부확률 : 사건 B가 일어난 상태에서 사건 A가 일어날 확률
→ 𝑃(𝐴|𝐵)
- 합의 법칙 : 두사건 A와 B가 서로 베타적(두 사건이 동시에 발생하지 X)이라면, A 또는 B 확률
◆ 확률 분포
: 확률 변수가 취할 수 있는 값들과 그 값들이 발생하는 확률
1) 이산 확률 분포 (Discrete Probability Distribution)
: 확률변수가 취할 수 있는 값이 개별적이고 셀수 있는 경우 (확률 값의 총합 = 1)
2) 연속 확률 분포 (Continuous Probability Distribution)
: 확률변수가 연속적인 범위의 값(실수범위의값)을 취할 수 있을 때 적용 (확률변수 전 구간의 적분값 = 1)
- 변수의 범위가 실수이므로 딱 하나의 구체적인 값에 대한 확률 = 0
- 정규분포
- 평균이 0, 표준편차가 1인 정규분포를 표준정규분포
◆ 확률 변수
: 실험, 관찰 또는 무작위 과정의 결과로 나타날 수 있는 수치적인 값
- 확률 분포의 영향을 받음
- 확률 분포를 알고 있다면 활률 변수를 임의로 생성할 수 있으며 이러한 과정을 샘플링(Sampling)이라고 함
-
특정 분포 𝐷를 따르는 확률 변수 𝑋를 n개 샘플링하면 아래와 같이 표현 가능

- ex) 동전 던지기 분포에서 하나의 데이터를 샘플링 하면 앞면이 나왔고 정규 분포에서 하나의 데이터를 샘플링 해서 나온 값은 0.02421 나왔다.
확률론적 모델링
: 주어진 데이터를 확률 이론의 관점에서 해석하고 모델을 설계하는 과정
= 수학적 모델로 데이터를 분석&활용하는 과정
- 데이터가 특정 확률 분포를 따른다고 가정
► (데이터에 존재하는 불확실성(noise)을 인정하면서) 이 분포는 데이터의 특성을 분석하거나 미래의 사건에 대한 예측에 활용됨
◆ 모델의 예측과 데이터
- 머신 러닝 모델의 출력은 확률론적 관점에서 예측된 결과물
► 따라서, 실제 결과물과 차이가 있을 수 있음

- ŷ : 모델의 예측
- y : 실제 정답(종속 변수)
- X : 입력 데이터(독립 변수)
-
► X와 y를 포함해서 일반적으로 전체 학습 데이터라고 한다.
