AB 테스트 시스템 구성
1. 런타임 시스템
- 사용자가 들어오면 A로 들어갈지 B로 들어갈지 결정하는 것
- Bucket을 결정하는 로직은 데이터 분석가가 정함
- AB 테스트 사용자 Bucket 정보를 ETL로 적재

2. 분석 시스템
- 이를 분석하기 편한 하나의 테이블로 JOIN
- Tableu와 같은 시각화 툴을 통해 분석
AB 테스트 시스템 구현 방법
1. 직접 구현
2. SaaS 활용
- Optimizely
- VWO
- Front End 관련 테스트
AB 테스트 프로세스
1. AB 테스트로 증명할 가설 제안 및 승인
2. AB 테스트 실행 및 QA
3. Rollout
4. Iterations
- 주간 AB 테스트 리뷰 미팅
- 대시보드 활용(Tableu, Looker, Power BI, Python Notebook 등)
- 애자일하게 진행 (전체 서비스 개발의 속도 증진을 위해)
- Ramp-up : 신규 기능의 결과가 좋다면 테스트 퍼센트를 증가(1% → 5% → ... → 100%)
◆ QA의 중요성
- AB 테스트는 개발자 혹은 디자이너에 의해 구현됨
- 그 과정에서 AB 테스트 제안자의 생각이 제대로 반영되지 않을 수 있음
- 주기적으로 AA 테스트를 수행해야 함
◆ 새로운 기능의 점진적 커버리지 확대
- AB 테스트 결과가 전체적으로는 안좋지만 특정 사용자 층에 대해서만 좋은 경우
→ AB 테스트 결과를 다양한 세그먼트의 사용자 별로 살펴봐야 함
◆ AB 테스트 진행 기간
- 기본적으로 일주일은 테스트 해야 함
- 많은 테스트들이 초반에는 통계적 유의미한 차이를 보이다가 시간이 지나면서 사라짐 →Data Peeking Problem
- 웹 스케일에서는 z-test 등의 전통 통계학에서 사용하는 최소 샘플의 크기가 의미 없음
- 가설의 일부로 원하는 지표의 성공/실패 기준에 따라 최소 트래픽 기준을 미리 설정하는 것이 좋음
- 사용자들이 익숙한 UI/UX의 변경은 최소 2-4주 실행해야 함
Traffic을 A와 B로 나누는 방법
AB 테스트의 성격에 따라 user id를 사용할지 device id를 사용할지 결정해야 한다.
- 로그인한 사용자에게만 하는 테스트 → user id 사용
- 모든 방문자에게 하는 테스트 → device id 사용
User ID
: 서비스에 사용자 등록이 되는 순간부터 부여되는 고유한 아이디
Device ID
: 로그인과 상관없이 서비스 방문자에게 부여되는 아이디로, 보통 브라우저 쿠키를 이용해서 생성됨
- 브라우저 쿠키가 reset 되는 순간 다시 생성됨
- 사용자가 아닌 브라우저를 고유하게 지칭
- 하나의 User ID가 여러 개의 Device ID를 가질 수 있음
- 하나의 Device ID가 여러 개의 User ID를 가질 수 있음
- 단순 크롤링/스크래핑을 하는 봇의 경우 쿠키 지원 X → Device ID 정보 없음
◆ 나누는 방법
1. 미리 모든 사용자를 A/B로 나누는 방법
- 로그인한 사용자를 대상으로 하는 경우 가능
- 다양한 각도에서 bias 제거 가능
- 비로그인 사용자 대상의 AB 테스트, AB 테스트 중 신규 등록 사용자는 불가능
2. 사용자를 동적으로 AB 테스트 진행중에 나누는 방법
- 일반적으로 사용됨
- 사용자의 로그인 여부와 상관 없이 적용 가능
- bias, interaction 발생 가능성 존재
◆ 나누는 프로세스
- 트래픽(User ID 혹은 Device ID)를 랜덤한 숫자 값으로 변환 (보통 MD5 사용)
- 바뀐 값(10진수)을 16진수로 변환
- 변환한 숫자에 나머지(modulo) 연산을 수행
- 나머지가 0이면 A, 나머지가 1이면 B로 나눔
◆ Python으로 구현
1) 필요한 라이브러리 불러오기
import psycopg2
import pandas as pd
import pandas.io.sql as sqlio
import math
2) Redshift connection 함수 정의
def get_Redshift_connection(autocommit):
host = "호스트 정보"
redshift_user = "유저 아이디"
redshift_pass = "유저 비밀번호"
port = 포트 번호
dbname = "dev" # 데이터베이스 이름
conn = psycopg2.connect("dbname={dbname} user={user} host={host} password={password} port={port}".format(
dbname=dbname,
user=redshift_user,
password=redshift_pass,
host=host,
port=port
))
conn.set_session(autocommit=autocommit)
return conn
conn = get_Redshift_connection(True)
cur = conn.cursor()
sql = """SELECT * FROM raw_data.aa_example"""
df = sqlio.read_sql_query(sql, conn)
df.head()
3) 트래픽 분리 과정을 함수로 구현
import hashlib
# 트래픽 분리 과정을 함수로 구현
def split_userid(id):
"""Given an id and the number of variants, returns a bucket number"""
h = hashlib.md5(str(id).encode())
return int(h.hexdigest(), 16) % 2 # num_of_variants
# 트래픽 분리 결과 보기
print(split_userid(100))
print(split_userid(101))
📌 문제점
- 모든 사용자들을 대상으로 50:50으로 나눔 → 점진적인 커버리지를 늘려가며 사용자 버킷팅이 필요함
- AB 테스트에 관계 없이 사용자들은 항상 A 혹은 B에 들어감 → bias 발생
◆ 개선된 Python으로 구현
► `md5`로 새로운 숫자를 만들어낼 때 `abtest_id` 추가
def split_userid(abtest_id, user_id, size_of_test, num_of_variants=2):
id = user_id + abtest_id
h = hashlib.md5(str(id).encode())
if (int(h.hexdigest(), 16) % 100) < size_of_test:
return int(h.hexdigest(), 16) % num_of_variants
else: # AB테스트에 포함되지 않는 경우 -1 리턴
return -1
◆ SQL로 구현
sql = """
SELECT 100 user_id, MOD(STRTOL(LEFT(MD5(100),15), 16), 2) variant_id
UNION
SELECT 101 user_id,MOD(STRTOL(LEFT(MD5(101),15), 16), 2) variant_id
"""
df = sqlio.read_sql_query(sql, conn)
df.head()
AB 테스트 결과 분석
- 경험과 도메인 지식이 중요
- 가설을 잘 세워야 함
- 객관적이고 공개되어야 함
- AB 테스트를 제안한 사람이 분석하는 것은 좋지 않음 (wrong incentive)
- 다양한 사람들의 의견을 듣는 것이 중요
◆ Outlier가 AB 테스트에 미치는 영향
- 어느 서비스나 매출 등에 있어 큰 손(Whale User)들이 존재하는데, 이게 어떤 bucket에 들어가느냐에 따라 분석에 큰 영향을 끼침
- 봇 유저(scraper bot)가 한쪽으로 몰릴 경우 session, impression 등에 큰 영향을 끼침
► Whale User들의 retention과 churn rate(이탈율)을 살펴봐야 함
► AB 테스트 결과를 다양한 관점에서 봐라봐야함
► 실제 데이터를 관찰할 필요가 있음
◆ 잘못된 가설이 AB 테스트에 미치는 영향
- Survivorship Bias
- 지표를 잘못 선택할 경우
► 가설에 대한 많은 질문을 던져야 함
► 성공 실패의 기준으로 더 중요한 지표가 있는지 고민해야 함
◆ AB 테스트 성공의 경우 지표가 항상 좋아야 하는가
- 테스트에 따라 지표가 개선되지 않아도 성공으로 간주될 수있음
AB 테스트 분석 시각화
◆ 대시보드 요구 조건
- AB 테스트 전체 기간에 걸쳐 Key 지표가 비교 가능해야 한다.
- 일별로 Key 지표의 비교가 가능해야 한다.
- Key 지표의 경우 통계적으로 유의미한지 표시되어야 한다. (Color Coding)
- 트래픽(사용자) Meta Data가 있다면 이를 바탕으로 필터링 가능해야 한다.
◆ 분석 데이터 전처리
- AB 테스트 사용자 버킷 정보, 기타 성능 정보를 ETL로 데이터 웨어하우스에 적재
- DBT를 활용해서 ELT 진행 → AB 테스트 분석 테이블
- 대시보드 시각화 (Tableau, Power BI 등 활용)
📌 AA 테스트
가설 :
진행 방식 :
AB 테스트들 간의 Interaction(상호작용)
ex. 4명의 사용자를 대상으로 2개의 테스트를 동시에 진행한다고 가정해보자.
| User ID | Test1 (A1, B1) | Test2 (A2, B2) |
| 1 | A1 | A2 |
| 2 | A1 | A2 |
| 3 | B1 | B2 |
| 4 | B1 | B2 |
- (A1, B2), (B1, A2) 조합은 테스트되지 못함
- 즉, 두 테스트들이 독립적으로 테스트 되는 것이 아니다.
- 조합에 따라 결과가 다름
- 후처리를 통해 영향을 살펴봐야 함
- 버킷팅을 미리 하는 것도 권장
AB 테스트 Variant 크기 비교
: Variant 간의 트래픽 크기가 동일한지(=통계적 차이가 신뢰구간 95% 내에 있는지) 살펴보는 과정
► 이항분포(binomial distribution)을 따름
ex)
| A (Control) | B (Test) | |
| User Size(*) | 50 | 53 |
| Impressions(**) | 120 | 115 |
| Clicks | 10 | 15 |
| Converted | 3 | 1 |
| Revenue | 1 | 3 |
AB 테스트 분석에 사용되는 기본 통계
귀무가설(Null Hypothesis; H0) : A = B
대립가설(Alternative Hypothesis; H1) : A ≠ B
- 귀무 가설 기반의 AB 테스트 분석은 비교 대상이 되는 데이터가 정규 분포를 따름을 가정한다.
- 모든 데이터 가 정규분포를 따르지 않음 → CLT(중심극한정리)를 사용해서 정규분포로 변환할 수 있다.
- (B - A)를 계산하여 동일한지 아닌지 여부를 판단해야 한다.
- t-test를 사용해서 P-value 혹은 Z-score를 계산해서 판단
- 얼마나 발생하기 힘든 일인지 보는 것
- 정규분포라면 양끝단이 됨
- Z-score : 정규분포 그래프에서 X축이 가리키는 값
- P-value : Z-score이 나타내는 축까지 오른쪽부터 계산한 면적
- 중심극한 정리 (Central Limit Theorem to the Rescue; CLT) :
- 어떤 집단의 모집단이 정규분포를 따르지 않더라도, 그 모집단 중에서 최소 30개 이상의 샘플들의 평균이 정규 분포를 따른다면 나머지 모집단도 정규 분포를 따른다.
- 샘플의 크기가 클수록 정규분포에 더 가까워진다.
정규분포 (Normal Distribution) - Bell Curve
: 평균 = μ, 표준편차 = σ를 따른다.
표준 정규분포 (Standard Normal Distribution)
: 평균 = 0, 표준편차 = 1를 따른다. (그래프 면적 1)
| 신뢰구간 | z-score(x축) |
| 90% | 1.645 |
| 95% | 1.96 |
| 99% | 2.575 |
풀고자 하는 문제에 따라서 양측 검정(Two-sided)과 단측 검정(One-sided)이 다르게 나뉜다.
정규 분포를 기반으로 CLT 적용 실습 (Python)
1) 필요한 라이브러리 불러오기
import numpy as np
import seaborn as sns
import statistics as stat
2) 표준 정규 분포 데이터 생성하기
x = np.random.normal(size=10000)
stat.mean(x)
stat.stdev(x)
3) 시각화
sns.displot(x)
4) 정규분포 모집단에서 랜덤하게 샘플 추출하기
# replace=False : 여기서 샘플된 데이터들은 x에서 제거된다
x_sample = np.random.choice(x, size=10, replace=False)
x_sample
stat.mean(x_sample)
stat.stdev(x_sample)
► 1번만 샘플링 했기 때문에 모집단의 특성을 유지하지 않고 있다.
5) 여러번 샘플링하는 함수 정의
# 모집단 : population, 샘플 추출 개수(샘플크기) : sample_size, 샘플링 횟수 : n_samples
def sample_mean(population, sample_size, n_samples):
sample_means = []
for i in range(n_samples):
sample = np.random.choice(population, size=sample_size, replace=False)
sample_mean = stat.mean(sample)
sample_means.append(sample_mean)
print(stat.mean(sample_means),stat.stdev(sample_means))
return sample_means
sns.displot(sample_mean(x, 10, 10))
► 샘플 개수가 30개가 넘지 않는 매우 작은 개수이기 때문에 아직까지는 정규분포를 따르지 못한다.
# 샘플 개수를 2500개로 늘려서 다시 시각화
sns.displot(sample_mean(x, 2500, 2500))
6) Skewed(기울어진) 분포를 갖는 모집단에서 샘플링
from scipy.stats import skewnorm
s = skewnorm.rvs(12, size=10000) # 첫번째 값이 0이면 정규분포가 리턴됨
stat.mean(s)
sns.displot(s)
► 샘플의 개수가 적기 때문에 skewed(기울어진) 형태를 띈다.
# 샘플 개수를 늘려보자
sns.displot(sample_mean(s, 1000, 1000))
7) Multimodal(봉우리 2개) 분포를 갖는 모집단에서 샘플링
m = np.concatenate((np.random.normal(size=10000), np.random.normal(loc = 4.0, size=10000)))
stat.mean(m)
stat.stdev(m)
sns.displot(m)
► 샘플의 수가 적기 때문에 아직까지는 multimodal(봉우리가 2개)인 형태를 띈다.
# 샘플 개수를 늘려보자.
sns.displot(sample_mean(m, 1000, 1000))
8) Uniform(균등) 분포를 갖는 모집단에서 샘플링하기
u = np.random.uniform(size=10000)
stat.mean(u)
stat.stdev(u)
sns.displot(u, kde=False)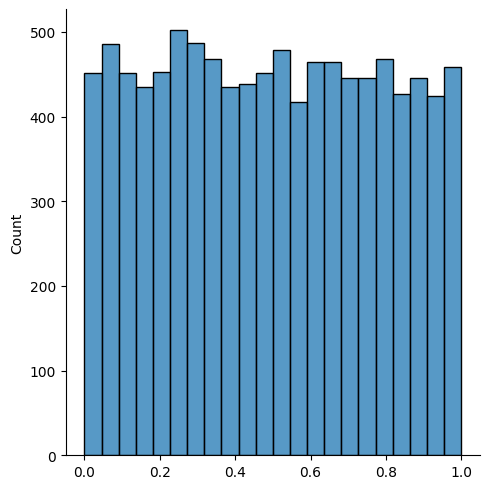
► 샘플의 수가 적기 때문에 Uniform(균일한)한 형태로 빽빽하게 채워진 형태를 띈다.
sns.displot(sample_mean(u, 1000, 1000))
AB 테스트 트래픽 크기의 통계적 비교
- 목표 : 트래픽이 양쪽에 원하는 형태로 나뉘어졌는가를 점검하는 것
- 귀무가설 : (50:50으로 나눈 테스트의 경우) P(A) = P(B) 혹은 P(B) = 0.5
- 사용할 검정 방법 : proportion z-test(혹은 one-sample t-test)로 유의수준(p-value)를 계산
비율 비교 : Proportion z-test
: 하나의 모집단에서 N개 샘플링으로 나온 특정 이벤트의 확률의 평균이 P일 때 P'라는 확률과 통계적으로 같은지 다른지 z-score을 비교
ex)
P = 테스트 사용자 B의 비율
P' = 0.5
N = 전체 사용자 수(A+B)
► (95% 신뢰도의 경우) -1.96 ≤ z-score ≤ 1.96 : A와 B의 트래픽 크기가 양쪽에 50%씩 나뉘어져 있음(우리가 원하는 형태)
► (95% 신뢰도의 경우) 1.96 < z-score, z-score < - 1.96 : A와 B의 트래픽 크기가 양쪽에 50%씩 나뉘지 못함 (발생하기 힘든일이 발생)
두 그룹의 평균 비교 : t-test
- One-sample t-test : z-test와 사실상 동일하지만 비율을 계산하는 것이 아님
- Two-sample t-test : 값들의 리스트를 비교할 때 사용
AA 테스트를 통한 검증
: AB 테스트의 시스템이 제대로 구현되었는지 보기 위해서 동일한 환경에 노출된 사용자들을 50:50으로 나누고 테스트한 후, 비교할 지표들을 계산해서 그 값들이 통계적으로 동일한지 아닌지를 검증
| A | A' | |
| Impressions | 10,000 | 10,500 |
| Clicks | 500 | 480 |
| Enrollment(Revenue) | 15 | 16 |
| Consumption and NPS | 11 | 12 |
► A와 A'가 통계적으로 무의미한 차이가 나야한다.
실습1. AB 테스트 트래픽 통계적 비교
사용할 데이터
# SQL 실행 후 결과를 pandas dataframe 형태로 불러오기
df = sqlio.read_sql_query("SELECT * FROM raw_data.aa_example LIMIT 10", conn)
df.head()
AA 테스트로 비교 (SQL)
A와 B에 속한 사용자 수와 세션 수 카운트하기
sql = """
SELECT
MOD(STRTOL(LEFT(MD5(user_id),15), 16), 2) variant_id,
COUNT(DISTINCT user_id) user_sum, // 그룹에 속한 사용자 수
COUNT(1) session_sum
FROM (
SELECT DISTINCT user_id, date
FROM raw_data.aa_example
)
GROUP BY 1; // 같은 variant_id에 속한 사용자들끼리 그룹화
"""
df = sqlio.read_sql_query(sql, conn)
df.head()
► `user_sum` 2056과 2070이 (예)신뢰구간 95% 내에서 통계적으로 같다고 할 수 있나?
AA 테스트 비교 (Python)
앞서 만든 `split_userid` 함수를 호출하여 A와 B에 속한 사용자 수와 세션 수 카운트하기
sql = """SELECT DISTINCT user_id
FROM raw_data.aa_example
"""
df = sqlio.read_sql_query(sql, conn)
df.head()
import hashlib
def split_userid(id, num_of_variants=2):
h = hashlib.md5(str(id).encode())
return int(h.hexdigest(), 16) % num_of_variants
a_user_count = 0
b_user_count = 0
for index, row in df.iterrows():
if split_userid(row["user_id"]) == 0:
a_user_count += 1
else:
b_user_count += 1
print(a_user_count, b_user_count)
► `a_user_count`2104와 `b_user_count` 2022가 (예)신뢰구간 95% 내에서 통계적으로 같다고 할 수 있나?
실습2. AB 테스트 Variant 크기 검증
= B에 속한 사용자 수가 0.5인지를 검증하는 것
[실습1 - SQL] 에서
- A 사용자수 = 2070
- B 사용자수 2056
- N = 2070 + 2056 = 4126
- 비교대상 확률 = 0.5
- P(B) = 2056/4126 = 0.498
- z-score = (P-0.5) / sqrt(P*(1-P)/N) = (0.498 - 0.5) / sqrt(0.498 * (1-0.498) / 4126) = -0.217
► z-table에 따르면 p-value = 0.4129 > 0.5
► 귀무가설 채택 (= B 사용자의 비율은 50%라고 할 수 있다.)
Python으로 해보기
1) One-sampled t-test
from scipy import stats
import math
def compute_zscore(n_test, n_ctrl, m_ctrl=0.5):
sum = n_test + n_ctrl
m_test = n_test/sum
s_test = math.sqrt((m_test-m_test*m_test)/sum)
z_score = (m_test-m_ctrl)/s_test
return z_score
math.sqrt(0.49830344159*(1-0.49830344159)/4126)
n_test = 2056
n_ctrl = 2070
print("A & B user traffic comparison", compute_zscore(n_test, n_ctrl))
2) Scipy 모듈 사용해서 계산
from scipy import stats
stats.ttest_1samp(a, 0.5)
3) Proportion z-test
from statsmodels.stats.proportion import proportions_ztest
n_test = 2056 # 테스트(B)에 속한 샘플 크기
n_ctrl = 2070 # 컨트롤(A)에 속한 샘플 크기
stats, pvalue = proportions_ztest(n_test, n_ctrl+n_test, value=0.5, alternative='two-sided')
print(stats, pvalue)
