[TIL] 데이터분석 데브코스 49일차 (1) - K-means Clustering(K-평균 군집화)/로이드 알고리즘(Lloyd's Algorithm)/엘보우 방법(Elbow Method)/SSE (Sum of Squared Errors)/실루엣 계수(Silhouette Coefficient)
K-means Clustering (K-평균 군집화)
: 전체 데이터를 K개의 덩어리(클러스터)로 나누는 비지도 학습법
- K : 클러스터(덩어리)의 개수
- 중심점(△) : 클러스터 안에 포함된 데이터들의 평균값
K-means Clustering을 푸는 알고리즘
- 로이드(Lloyd) 알고리즘
- 엘칸(Elkan) 알고리즘
: 데이터 포인트와 클러스터 중심 거리를 계산하는 과정에 삼각 부등식을 사용 (|𝑎| + |𝑏| ≤ |𝑎| + |𝑏|)
로이드 알고리즘 프로세스
1단계. 초기화
K개의 클러스터 중심점을 데이터 내에서 임의로 선택한다.
- 초기 위치는 최종 결과에 큰 영향을 미칠 수 있음
- k-means++ 초기화 방법 많이 사용
📌 k-means++ 초기화 방법
초기 중심점 위치를 서로 멀리 떨어지게 설정 ► 임의의 랜덤 위치보다 좋은 결과
2단계. 할당
모든 각각의 데이터 포인트들에 대해서 중심점과의 거리를 계산해서 가장 가까운 클러스터 중심점에 할당한다.
- 일반적으로 유클리드 거리 사용

- or 코사인 유사도 or 맨해튼 거리
3단계. 업데이트
: 할당 이후에 각 클러스터에 속한 데이터들의 평균점 위치로 클러스터 중심점 위치를 갱신한다.
4단계. 반복
위의 2~3단계 과정을 클러스터 중심점의 변화가 거의 없을때 까지 반복한다.
변화가 없다 :
- 위치의 변화가 없음
- 클러스터에 할당되는 데이터 포인트의 변화가 없음
- 동일한 데이터 포인트 할당 과정이 반복
- 지정된 횟수에 도달
K-means Clustering 실습
1단계. 데이터 생성
`make_blobs` : 클러스터링 용 데이터 생성 함수
- `centers` : 클러스터(혹은 중심점)의 개수
- `cluster_std` : 각 클러스터의 퍼짐 정도
- `n_features` : 사용할 feature의 개수
## 데이터 생성
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
seed = 1234
np.random.seed(seed)
# 가상 데이터 생성
X, y_true = make_blobs(n_samples=300,
centers=4, # Cluster의 수 혹은 Cluster의 중심 위치 좌표
cluster_std=0.60, # 각 클러스터가 얼마나 퍼져있게 할건지
n_features=2, # 사용할 feature의 수, 시각화를 위해 2차원 사용
random_state=0)
# 데이터 시각화
plt.scatter(X[:, 0], X[:, 1], s=20)
plt.title("Generated Data")
plt.show()
2단계. K-means 클러스터링 진행
`KMeans` : K-means 클러스터링을 수행하는 함수
- `n_clsuters` : 클러스터 개수
- `init` : 초기 클러스터 중심점을 잡는 초기화 방법(일반적으로 `'k-means++'` 사용)
- `n_init` : 초기 중심점 잡기를 할 횟수
from sklearn.cluster import KMeans
# K-Means 클러스터링 수행 (k=4)
kmeans = KMeans(n_clusters=4,
init='k-means++', # 초기 클러스터 중심 위치를 잡는 초기화 방법
n_init=10, # 초기 중심점 잡기를 얼마나 많은 다른 방법으로 설정할지를 결정 / 10번의 시도를 하겠다는 것이고, 10번 중 최고의 SSE 성능을 보이는 모델을 최종 모델로 사용
random_state=0)means.fit(X)
y_kmeans = kmeans.predict(X)
시각화
# 클러스터링 결과 시각화
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=20, cmap=plt.cm.Paired)
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.5, marker='^')
plt.title("KMeans Clustering (k=4)")
plt.show()
엘보우 방법(Elbow Method)
: 최적의 K값을 선택하는 방법으로, 클러스터 수를 늘려가며 각각에 대한 클러스터링 성능을 SSE 값으로 SSE의 감소율이 급격히 줄어드는 지점(= 가장 좋은 성능을 나타내는 곳)을 찾는 방법
# 1~10 까지의 K를 설정하고 각 경우에 맞춰 학습을 진행
inertia = []
K_range = range(1, 10)
for k in K_range:
kmeans = KMeans(n_clusters=k, init='k-means++', n_init=10, random_state=0)
kmeans.fit(X)
inertia.append(kmeans.inertia_) # SSE 값을 저장
plt.figure(figsize=(8, 4))
plt.plot(K_range, inertia, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
plt.title('Elbow Method')
plt.show()
클러스터링의 성능 평가 지표
1. SSE (Sum of Squared Errors)
: 각 클러스터 내 데이터 포인트와 클러스터 중심점 간의 거리의 제곱 합
2. 실루엣 계수(Silhouette Coefficient)
: 클러스터 안의 응집도와 서로 다른 클러스터 간의 분리도를 동시에 고려해 군집화의 품질을 평가하는 방법
- 값이 클수록 좋은 클러스터링
- -1 ≤ 𝒔(𝒊) ≤ +1
-

- 응집도(Cohesion) : 𝒂(𝒊)
- 특정 데이터 𝑖에 대해, 동일한 클러스터 안에 들어있는 다른 데이터들과의 평균 거리
- 클러스터 내부의 데이터가 얼마나 모여있는지를 나타냄 (작을수록 좋음)
- ex) 같은 반 아이들끼리의 친밀도
- 분리도(Separation) : 𝒃(𝒊)
- 특정 데이터 𝑖 에 대해, 𝑖가 들어있는 클러스터 말고, 다른 클러스터 중 가장 가까운 클러스터 중심까지 거리
- 다른 클러스터와 얼마나 떨어져 있는지를 나타냄 (클수록 좋음)
- ex) 다른 반 아이들과의 친밀도
- 최대값 : 1 → 𝑎(𝑖)가 거의 0에 근접해 𝑏(𝑖)만 남는 상황 = 제일 좋은 상황
- 최소값: -1 → 𝑏(𝑖)가 값이 작아지고 오히려 𝑎(𝑖)가 커지는 경우 = 제일 나쁜 상황
from sklearn.metrics import silhouette_score
silhouette_avg = silhouette_score(X, y_kmeans)
print("Silhouette Score: {:.2f}".format(silhouette_avg))
K-means Clustering 실습
실습 데이터
🔗 실습 링크 : https://www.kaggle.com/datasets/kandij/mall-customers/
Mall customers
We use K-means clustering algorithm majorly in this kernel.
www.kaggle.com
| 변수명 | 의미 |
| CustomerID | 고객 ID - 수치형 데이터 - 고유 식별자 (학습에서 제외) |
| Genre | 성별 - 범주형 데이터 - 전처리로 인코딩 과정 필요 |
| Age | 나이 - 수치형 데이터 - 각자 서로 다른 스케일을 갖고 있음 - 거리 기반 군집화에서 스케일 매칭이 매우 중요 |
| Annual Income | 연간 소득 - 수치형 데이터 - 각자 서로 다른 스케일을 갖고 있음 - 거리 기반 군집화에서 스케일 매칭이 매우 중요 |
| Spending Score | 쇼핑 점수 - 수치형 데이터 - 각자 서로 다른 스케일을 갖고 있음 - 거리 기반 군집화에서 스케일 매칭이 매우 중요 |
문제 정의
: 주어진 [독립변수]고객 데이터를 바탕으로 고객을 세분화(Customer Segmentation) 군집화
(but, 군집화를 해야하는 명확한 이유가 필요함!)
1단계. 데이터 로드
import numpy as np
seed = 1234
np.random.seed(seed)import pandas as pd
# 데이터 경로 지정 및 읽어오기
data_path = '/content/Mall_Customers.csv'
customers = pd.read_csv(data_path)
# 데이터 꼴 확인
customers.head()
2단계. EDA
1) 기본 정보 및 기초 통계량 분석
# 기본 정보
print('#'*20, '기본 정보', '#'*20)
customers.info() # info() 안에서 자동으로 print를 진행
# 기초 통계량
summary_statistics = customers.describe(include='all')
print('#'*20, '기초 통계량', '#'*20)
print(summary_statistics)

2) 시각화 - 범주형 데이터
# 성별 데이터 분포 확인
category_columns = ['Genre']
category_data = customers[category_columns]
import matplotlib.pyplot as plt
plt.figure(figsize=(4, 4))
np.random.seed(seed)
col = (np.random.random(), np.random.random(), np.random.random())
customers['Genre'].value_counts().plot(kind='bar', color=col)
plt.title('Female VS Male')
plt.tight_layout()
plt.show()
3) 시각화 - 수치형 데이터
# 데이터 가져와서
numeric_columns = ['Age', 'Annual Income (k$)', 'Spending Score (1-100)']
numeric_data = customers[numeric_columns]
# 분포 시각화
plt.figure(figsize=(18, 4))
np.random.seed(seed)
for idx, numeric in enumerate(numeric_columns) :
col = (np.random.random(), np.random.random(), np.random.random())
plt.subplot(1, 3, idx+1)
plt.hist(numeric_data[numeric], bins=50, color=col, edgecolor='black')
plt.title(numeric)
plt.tight_layout()
plt.tight_layout()
plt.show()
4) 이상치 확인 - 수치형 데이터
# 아웃라이어 확인
plt.figure(figsize=(12, 4))
np.random.seed(seed)
for idx, numeric in enumerate(numeric_columns) :
plt.subplot(1, 3, idx+1)
plt.boxplot(numeric_data[numeric].dropna(), labels=[numeric])
plt.tight_layout()
plt.show()
5) 상관관계 분석 - 수치형 데이터
# 상관관계 메트릭스
correlation_matrix = numeric_data.corr()
# 상관관계 메트릭스 시각화
plt.figure(figsize=(4, 4))
plt.matshow(correlation_matrix, fignum=1)
plt.colorbar()
plt.xticks(range(len(correlation_matrix.columns)), correlation_matrix.columns, rotation=90)
plt.yticks(range(len(correlation_matrix.columns)), correlation_matrix.columns)
for (i, j), val in np.ndenumerate(correlation_matrix):
plt.text(j, i, '{:0.2f}'.format(val), ha='center', va='center', color='black')
plt.show()
3단계. 데이터 전처리
1) 결측치 제거
# 결측치 값 존재 여부 확인
exist_na = customers.isna().values.any()
exist_null = customers.isnull().values.any()
print(exist_na, exist_null)
2) 범주형 변수 인코딩 - One-hot Encoding
# 성별을 이진 변수로 변환
encoding_map = {'Female': 1, 'Male': 0}
categori_data_encode = pd.DataFrame(customers['Genre'].replace(encoding_map))
categori_data_encode.columns = ['Gender']
categori_data_encode
3) 수치형 데이터 스케일링 - Standard Scaling
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
# 수치형 데이터 스케일링
numeric_data = customers[numeric_columns]
numeric_data_scaled = scaler.fit_transform(numeric_data)
numeric_data_scaled = pd.DataFrame(numeric_data_scaled)
numeric_data_scaled.columns = numeric_columns
numeric_data_scaled
4) 전처리된 데이터 합쳐주기
customers_combined = pd.concat([numeric_data_scaled,
categori_data_encode],
axis=1)
customers_combined
4단계. K-means clustering 모델 구축
1) 최적의 K값 찾기 - Elbow Method (with SSE, Silhouette score)
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
inertia, silhouette = [], []
K_range = range(2, 11)
for k in K_range:
kmeans = KMeans(n_clusters=k, init='k-means++', n_init=10, random_state=0)
kmeans.fit(customers_combined)
inertia.append(kmeans.inertia_)
y_kmeans_silhouette = kmeans.predict(customers_combined)
silhouette.append(silhouette_score(customers_combined, y_kmeans_silhouette))plt.figure(figsize=(8, 10))
plt.subplot(2, 1, 1)
plt.plot(K_range, inertia, label='SSE', marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
plt.title('Elbow Method - SSE')
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(K_range, silhouette, label='Silhouette', marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Silhouette')
plt.title('Elbow Method - Silhouette')
plt.legend()
plt.show()
# 최대 실루엣 계수의 값을 갖는 cluster의 수
max_shil = max(silhouette)
best_depth = K_range[silhouette.index(max_shil)]
print(f'최대 실루엣 계수 값을 갖는 cluster는 {best_depth} 개')
► 알 수 있는 정보
- SSE : K=4 혹은 K=6에서 감소율 변화가 보임
- 실루엣 계수 : K=6에서 최고 값을 갖음
∴ 최적 K=6으로 선택 - 실루엣 계수의 변동이 있는 것은 매우 일반적인 현상
- 데이터 구조의 복잡성
- 잡음과 이상치
- 균일하지 않은 밀도 & 데이터 간 거리
- 실루엣 계수간 차이가 크지 않다면 작은K를 기준으로 하는게 좋은 선택
2) 모델 학습시키기
kmeans = KMeans(n_clusters=6,
init='k-means++',
n_init=10,
random_state=0)
kmeans.fit(customers_combined)
5단계. 학습한 모델 평가
y_pred = kmeans.predict(customers_combined)
silhouette_avg = silhouette_score(customers_combined, y_pred)
print("SSE Value : {:.2f}".format(kmeans.inertia_))
print("Silhouette Score: {:.2f}".format(silhouette_avg))
►알 수 있는 정보
- 실루엣 계수가 0.3을 넘었으므로 나쁘지 않은 성능
- SSE로는 잘 모르겠음
∴ SSE와 실루엣 계수만으로는 성능을 파악할 수 없다. 따라서 시각화를 통해서 알아봐야한다.
6단계. 결과 해석
1) 시각화를 위해 데이터 차원 변환
우리가 사용한 4차원 데이터(age, income, genre, spending score)는 바로 시각화할 수 없음
► 따라서, 시각화를 위해 2차원 데이터로 변환 (t-SNE 알고리즘 활용)
# 우리가 사용한 4차원 데이터(age, income, genre, spending score)를 시각화하기 위해 2차원 데이터로 변환 (t-SNE 알고리즘 활용)
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, random_state=seed)
customers_tsne = tsne.fit_transform(customers_combined)
# 2차원으로 변화된 데이터에 feature 이름을 넣어주고
# K-means가 예측한 각 데이터의 클러스터링 인덱스를 제공
customers_tsne_df = pd.DataFrame(data=customers_tsne, columns=['TSNE1', 'TSNE2'])
customers_tsne_df['Cluster'] = y_pred
customers_tsne_df
# 시각화
np.random.seed(seed)
plt.figure(figsize=(10, 8))
for idx in range(kmeans.n_clusters):
_color = (np.random.random(), np.random.random(), np.random.random())
cluster_data = customers_tsne_df[customers_tsne_df['Cluster'] == idx]
plt.scatter(cluster_data['TSNE1'],
cluster_data['TSNE2'],
color=_color,
label=f'Cluster {idx+1}',
marker='o')
plt.title('Customer Segments - t-SNE 2D')
plt.legend()
plt.show()
2) 각 클러스터 별 의미 찾기
만들어진 클러스터가 어떤 의미가 있는지 도메인 지식을 이용해 추측해야 한다.
- 원래 데이터의 형태로 전처리의 역과정을 거쳐 데이터의 재건한 뒤
- 각 클러스터에 포함된 데이터의 의미를 확인해야 함
- 간단하게 기본 정보 혹은 기술통계를 확인
- 상관관계 분석, 다른 머신러닝 모델 생성 등의 과정이 필요
# 원래 데이터에서 재건하기
customers_combined['Cluster'] = kmeans.labels_
# 수치형 데이터 스케일링 작업을 역으로 수행하기
original_numeric_data = pd.DataFrame(scaler.inverse_transform(customers_combined[numeric_columns]))
original_numeric_data.columns = numeric_columns
# 범주형 데이터 역 인코딩 (필요시)
# 수치형으로 되어있던 데이터를 다시 범주형으로 바꾸면 특성 파악이 눈에 안들어올 수 있음!
reverse_encoding_map = {v: k for k, v in encoding_map.items()}
original_category_data = pd.DataFrame(customers_combined['Gender'].replace(reverse_encoding_map))
original_category_data.columns = category_columns
# pandas로 원래 데이터 다시 만들기
labeled_origin_date = pd.concat([customers_combined['Cluster'],
original_numeric_data,
customers_combined['Gender']],
# original_category_data], # 범주형 데이터 필요시 사용
axis=1)
labeled_origin_date
# 각 군집에 대한 기술통계 계산
cluster_description = labeled_origin_date.groupby('Cluster').describe().transpose()
# 군집별 평균값
cluster_means = labeled_origin_date.groupby('Cluster').mean().transpose()cluster_description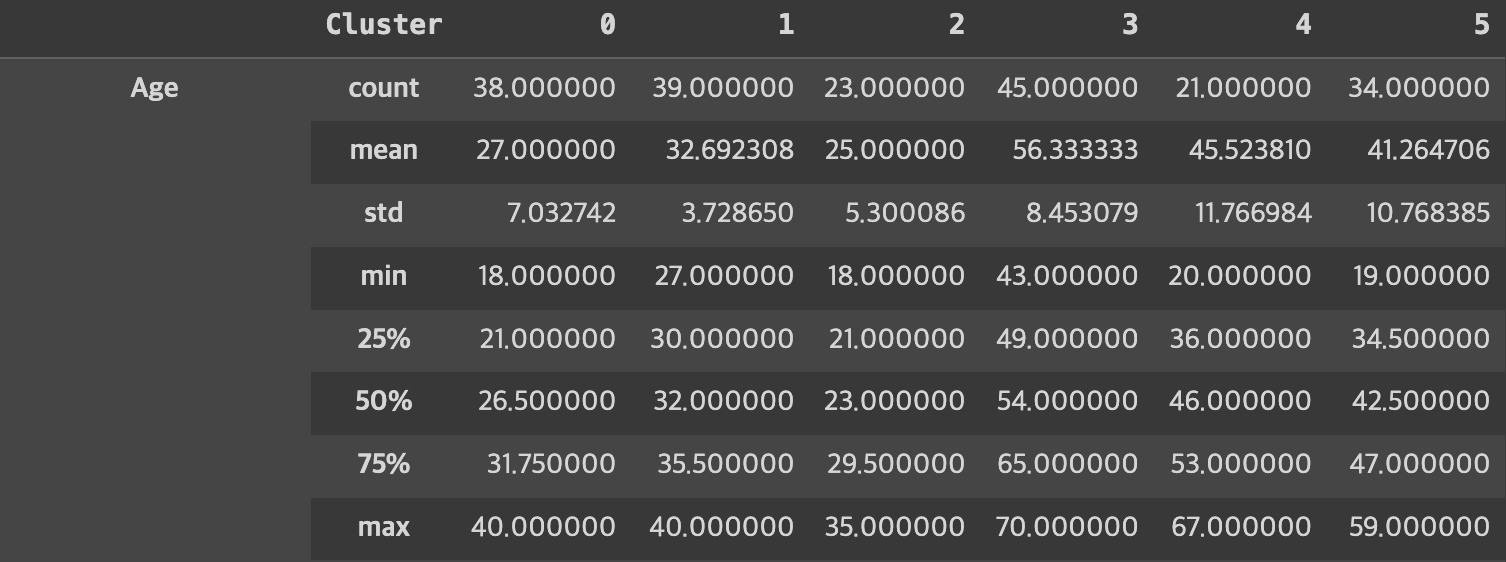



cluster_means